CentOS 7

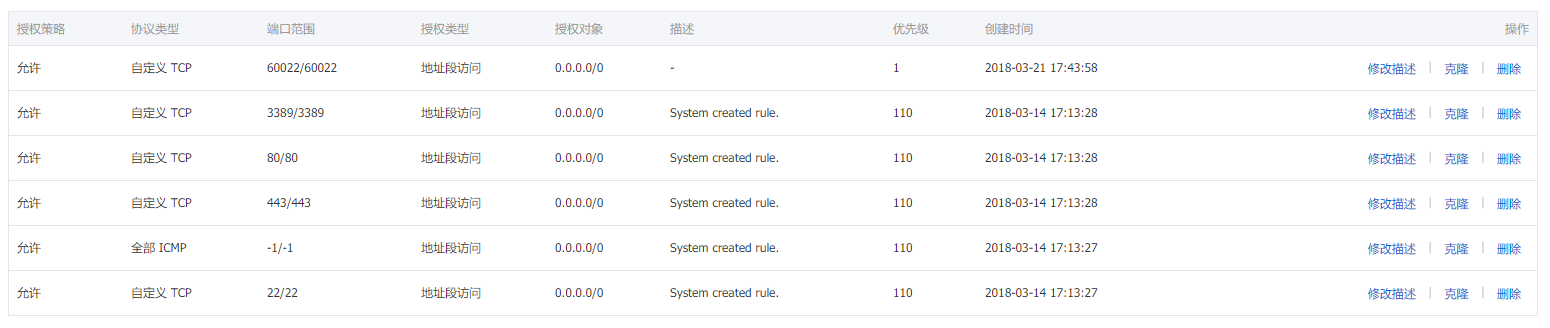
修改SSH默认端口22

SSH远程登录部分可参见SSH原理与运用。具体终端命令可参见怎样修改 CentOS 7 SSH 端口, 本质为修改开放端口+防火墙修改

如若和我一样为阿里云服务器, 则需要找到控制台中的安全组规则，自定义的开放想要SSH连接的端口，否则在Xshell等工具中仍然无法连接。

关闭账号密码登录

vi /etc/ssh/sshd_config

找到PasswordAuthentication yes，更改为no即可。此时再用一未信任的设备连接，可用终端命令登陆

ssh -p 22 hostName@address

提示以下错误信息则证明已无法直接通过账号密码直接登陆

Permission denied(publickey,gssapi-keyex,gssapi-with-mic).

Nginx搭建开发

Nginx的环境搭建可见Nginx Documentation，在配置SSH默认端口过程中可能将Nginx使用的默认80端口禁用，可参考Centos 7 firewall 命令在防火墙中打开对80的访问。

以免在服务器上预览开发效率过低，因此在本地也同时配置了Nginx，同时搭配Browsersync可以保证只要Web文件有修改时浏览器自动刷新，提高开发效率。

Nginx默认在80端口开放，因此启用代理模式可以实现类似Hexo主题开发中的效果。

browser-sync start --proxy "localhost:80" --files "**"

引号中的内容可更换为**.css等glob语法的正则表达式.

Git的自动化部署

Git的环境搭建可参见搭建Git服务器。由于更换了端口号，因此所有Git命令的对象都变为了类似git clone ssh://host@ip:port/xxx/xxx。

在配置完Nginx后，为了能git push后将整个repo拷贝到Nginx的指定网页文件夹中(默认为Nginx/html), 可参考VPS服务器搭建Hexo博客教程中的安装配置git部分实现Git Hook的功能。

如若为Windows平台，可能遇到push后post-receive文件无法自动执行的问题，因为行尾Unix与Windows格式不一，可在Sublime或其他文本编辑器中修改行尾为UNIX即可解决(其他无法执行原因可直接执行该脚本查看)

具体可以参考bad interpreter: No such file or directory

理解来自CSDN中的递归删除算法，个人补充细节描述

题为「设计递归算法，删除无头结点的单链表L中值为x的结点」

void deleteX(LinkList &L, ElemType x)  
{  
    LNode *p;  
    if(L==NULL) return;  
    if(L->data==x)  
    {  
        p=L;  
        L=L->next; // (1)单链表保持连续 
        free(p);  
        deleteX(L,x); // (2)递归调用
    }
    else
        deleteX(L->next,x); //(3)向后遍历
}  

理解难度在于似乎仅仅只是释放了当前结点并使得L向前推进，而导致了断链。

例如要在单链表$[1, 3, 5, 7]$中删除元素$x$(例如$x=3$)，这里递归第二次调用函数讲会遇到$data==3$

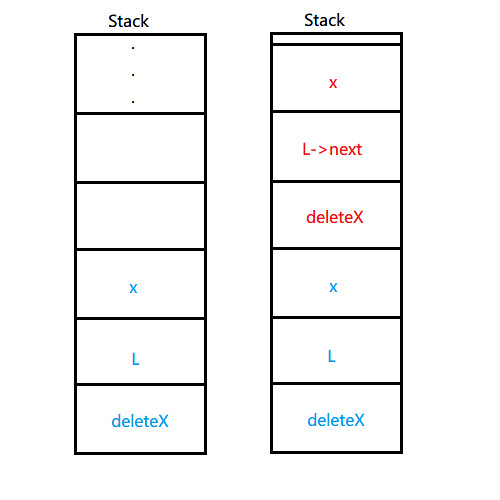
核心理解在于这里的LinkList L是引用, 观察堆栈会非常清晰的说明这个问题。

当代码中$(2)$处递归调用deleteX时, 参数作为L->next的引用传入(引用为别名，相当于本体操作)，即递归中参数L为上一函数的L->next本体，此时的代码相当于

deleteX(L->next, x)  
{  
    // ...
    p = L->next;  
    L->next = L->next->next; // 单链表保持连续 
    free(p);  
    deleteX(L->next, x);
    // ...
}  

如若将引用更换为指针，相较于引用的实现较为繁琐，但更能观察到上述代码工作的本质。

// 仅有传入指针的指针才能改变上一函数中指针的值
void deleteX(LinkList **L, ElemType x)  
{  
    LNode *p;  
    if((*L)==NULL) return;  
    if((*L)->data==x)  // L->next指向的结点为x
    {  
        p=*L;  // p指向L->next指向的结点
        *L=(*L)->next; // L->next=L->next->next
        free(p);  
        deleteX(L,x); // 传入L->next的地址
    }
    else
        deleteX(&((*L)->next),x); // 传入L->next指向的结点的next指针的地址
}  

坐标变换

通常摄像机动画，模型动画中会使用旋转平移变换来完成坐标变换。这里使用基变换来完成通用的坐标系转换。

现要求得世界坐标$P_{world}$对应的代求坐标系$\Omega$下坐标$P_{\Omega}$，已知$\Omega$坐标轴向量分别为$\overset{\rightharpoonup}{X}, \overset{\rightharpoonup}{Y}, \overset{\rightharpoonup}{Z}$,坐标原点为$O$

$worldToObject$
\left[
\begin{matrix}
\overset{\rightharpoonup}{X}.x & \overset{\rightharpoonup}{Y}.x & \overset{\rightharpoonup}{Z}.x & O.x \
\overset{\rightharpoonup}{X}.x & \overset{\rightharpoonup}{Y}.y & \overset{\rightharpoonup}{Z}.y & O.y \\
\overset{\rightharpoonup}{X}.z & \overset{\rightharpoonup}{Y}.z & \overset{\rightharpoonup}{Z}.z & O.z \\
0 & 0 & 0 & 1
\end{matrix}
\right]

即有$P_{\Omega}=worldToObject * P_{world}$.(该矩阵含义可展开其含义自明)

PBRT以及Atmos中关于相机各类坐标系的转换

PBRT中的NDC坐标系在Atmos中未使用，因为其本身在PBRT中并不直接体现

具体的转换管线流程如下，实现公式可由下图各自推导出来，不做赘述。

rasterPosition(imageX, imageY);

// raster to screen
screenPosition(rasterPosition.x - image->width / 2.0f, -rasterPosition.y + image->height / 2.0f);

// screen to camera
// 这里pbrt中使用投影矩阵的逆变换得到cameraPos，不过由于透视的特殊性，其方向向量是一致的。
cameraPosition.x = 2 * canvasSize.x * screenPosition.x / image->width;
cameraPosition.y = 2 * canvasSize.y * screenPosition.y / image->height;
cameraPosition.z = canvasDistance;

// camera to world
ray->direction = (cameraToWorld * cameraPosition).getNormalized();
ray->origin = cameraToWorld * zeroVector3;

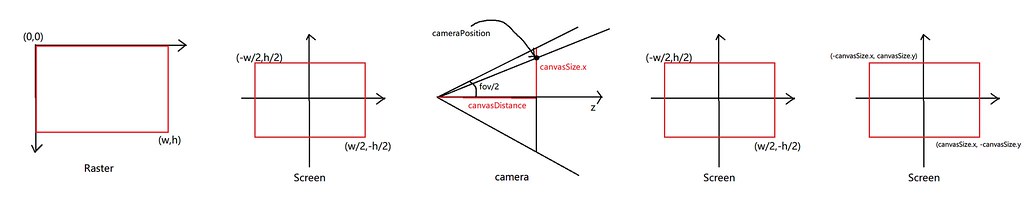
之后可以用worldToCamera矩阵进行转换。

$worldToCamera$
\left[
\begin{matrix}
right.x & up.x & direction.x & origin.x \
right.x & up.y & direction.y & origin.y \\
right.z & up.z & direction.z & origin.z \\
0 & 0 & 0 & 1
\end{matrix}
\right]

本文运用上文中多维随机变量分布转换规律，来推导出PBRT中一系列重要结论

极坐标与笛卡尔坐标

已知$p(x, y)=\frac{p(r, \theta)}{\vert J_t(r, \theta) \vert}$，其中
$\begin{array}{c}{T}_1(r,\theta )=rcos\theta =x\\ T_2(r,\theta )=rsin\theta =y\end{array}$
\begin{array}{l}
T_1(r,\theta)=rcos\theta=x \\
T_2(r,\theta)=rsin\theta=y
\end{array}

$J_t(r, \theta)=\left[$
\begin{matrix}
cos\theta & -rsin\theta \\
sin\theta & rcos\theta \\
\end{matrix}
\right] = r

则有$p(r, \theta) = rp(x, y)$

球坐标与笛卡尔坐标

$\begin{array}{c}{T}_1(r,\theta ,\varphi )=rsin\theta cos\varphi =x\\ T_2(r,\theta ,\varphi )=rsin\theta sin\varphi =y\\ T_3(r,\theta ,\varphi )=rcos\theta =z\end{array}$
\begin{array}{l}
T_1(r,\theta, \phi)=rsin\theta cos\phi = x \\
T_2(r,\theta, \phi)=rsin\theta sin\phi = y \\
T_3(r,\theta, \phi)=rcos\theta = z
\end{array}

则$p(x, y, z)=\frac{p(r, \theta, \phi)}{\vert J_t(r, \theta, \phi) \vert}$，其中

$J_t(r, \theta, \phi)=\left[$
\begin{matrix}
sin\theta cos\phi & rcos\theta cos\phi & -rsin\theta sin\phi \\
sin\theta sin\phi & rcos\theta sin\phi & rsin\theta cos\phi \\
cos\theta & -rsin\theta & 0\\
\end{matrix}
\right] = r^2sin\theta

则有$p(r, \theta, \phi) = r^2sin\theta p(x, y, z)$。

立体角与球坐标

立体角的定义为在单位圆上投影的面积，在球坐标中有$d\omega=sin\theta d\theta d\phi$成立

因此基于物理Lambertion中的$\int_{\Omega}{f(\omega_i, \omega_o, p)cos\theta d\omega}$=1, 可得$f(\omega_i, \omega_o, p) = \frac{1}{\int_{0}^{2\pi}d\phi \int_{0}^{\frac{\pi}{2}}{cos\theta sin\theta d\theta}} = \frac{1}{\pi}$

若定义在某区域$\Omega$上的概率为$Pr\{ \omega \in \Omega \} = \int_{\Omega}{p(\omega)d\omega}$，也有$Pr\{ (\theta ,\phi) \in \Omega '\} = \int_{\Omega '}{p(\theta, \phi)d\theta d\phi}$

因此
$p(\theta, \phi)d\theta d\phi=p(\omega) d\omega$
$p(\theta, \phi)=sin\theta p(\omega)$

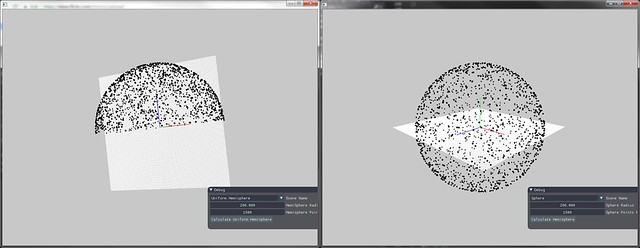
半球上立体角均匀采样

要对单位半球做关于立体角的均匀采样，则$p(\omega)=\frac{1}{2\pi}$，根据上文中与球坐标关系，$p(\theta, \phi)=\frac{sin\theta}{2\pi}$。

则有两独立同均匀分布随机变量$(\xi,\psi)\in [0,1]$，要转换成满足半球上均匀分布的球坐标表示。

$p(\theta) = \int_{0}^{\frac{\pi}{2}}p(\theta, \phi)d\phi = sin\theta, \quad p(\phi) = \int_{0}^{2\pi}p(\theta, \phi)d\theta = \frac{1}{2\pi}$

$p(\theta \vert \phi) = \frac{p(\theta, \phi)}{p(\phi)}=sin\theta, \quad p(\phi \vert \theta) = \frac{p(\theta, \phi)}{p(\theta)}=\frac{1}{2\pi}$

这里很明显可以看出来$\theta,\phi$为两个独立随机变量

$Pr\{\theta' \leqslant \theta\} = \int_{0}^{\theta}p(\theta)d\theta=1-cos\theta , Pr\{\phi' \leqslant \phi\} = \int_{0}^{\phi}p(\phi)d\phi=2\pi \phi$

应用反CDF变换法则，$P^{-1}(\theta)=1-arccos\theta, P^{-1}(\phi)=2\pi \phi$，因此
$\begin{array}{c}\theta =arccos(1-\xi )=arccos\xi \\ \varphi =2\pi \psi \end{array}$
\begin{array}{l}
\theta=arccos(1-\xi)=arccos\xi \\
\phi=2\pi \psi
\end{array}

由于球坐标不容易在计算机中表示，因此转换为笛卡尔表示

$\begin{array}{c}x=sin\theta cos\varphi =\sqrt{1-{\xi }^2}cos2\pi \psi \\ y=sin\theta sin\varphi =\sqrt{1-{\xi }^2}sin2\pi \psi \\ z=cos\theta =\xi \end{array}$
\begin{array}{l}
x=sin\theta cos\phi=\sqrt{1-\xi^2}cos2\pi \psi \\
y = sin\theta sin\phi = \sqrt{1-\xi^2}sin2\pi \psi \\
z = cos\theta = \xi
\end{array}

同理可推证球上立体角均匀采样

$\begin{array}{c}x=2\sqrt{\xi (1-\xi )}cos2\pi \psi \\ y=2\sqrt{\xi (1-\xi )}sin2\pi \psi \\ z=1-2\xi \end{array}$
\begin{array}{l}
x=2\sqrt{\xi(1-\xi)}cos2\pi \psi \\
y = 2\sqrt{\xi(1-\xi)}sin2\pi \psi \\
z = 1-2\xi
\end{array}

下图为半球上均匀采样的结果与完整球上均匀采样的结果

单位圆上的均匀采样

要根据面积对单位圆上进行均匀采样，$p(x,y)=\frac{1}{\pi}$，则$p(r, \theta)=rp(x,y)$。

$p(\theta)=\int_{0}^{1}\frac{r}{\pi}dr=\frac{1}{2\pi}, \quad p(r\vert \theta)=\frac{p(r,\theta)}{p(\theta)}=2r$

则他们对于的CDF为$P(\theta)=\int_{0}^{\theta}p(\theta)d\theta=\frac{\theta}{2\pi}$，$P(r\vert \theta)=\int_{0}^{r}p(r\vert \theta)dr=r^2$

求出其对应反函数$P^{-1}(\theta)=2\pi\theta$，$P^{-1}(r\vert \theta)=\sqrt{r}$

若有两满足在$[0, 1]$上均匀分布的随机变量$\xi, \psi$有$\theta=2\pi \xi, r=\sqrt{\psi}$

则转换回笛卡尔坐标结果为

$\begin{array}{l}$
x = \sqrt{\psi}cos2\pi \xi\\
y = \sqrt{\psi}sin2\pi \xi
\end{array}

这里$r, \theta$也是两个独立的随机变量

PBRT中论述的Concentric Disk Sampling可以参见前文Depth of Field中的实现与可视化

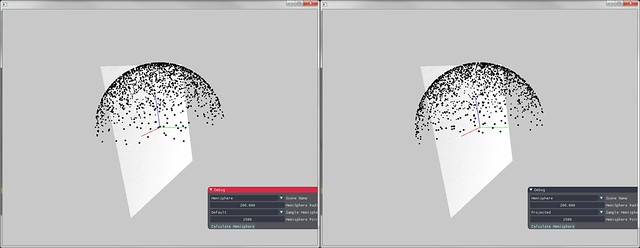
基于Cosine函数的半球采样

这里使用基本的转换思路，$p(\omega)\propto cos\theta$，因此$p(\omega)=\frac{cos\theta}{\pi}$

有$p(\theta, \phi)=\frac{sin\theta cos\theta}{\pi}$，则有

$p(\theta)=\int_{0}^{2\pi}p(\theta, \phi)d\phi=2sin\theta cos\theta, \quad p(\phi \vert \theta)=\frac{p(\theta, \phi)}{p(\theta)}=\frac{1}{2\pi}$

可得CDF为

$P(\theta)=\int_{0}^{\theta}p(\theta)d\theta=\frac{1-cos2\theta}{2}, \quad P(\phi \vert \theta)=\int_{0}^{\phi}p(\phi \vert \theta)d\phi=\frac{\phi}{2\pi}$

应用反CDF得$P^{-1}(\theta)=\frac{1}{2}arccos(1-2\theta), P^{-1}(\phi \vert \theta)=2\pi \phi$

$\begin{array}{c}\theta =\frac{1}{2}arccos(1-2\xi )\\ \varphi =2\pi \psi \end{array}$
\begin{array}{l}
\theta = \frac{1}{2}arccos(1-2\xi)\\
\phi = 2\pi \psi
\end{array}

转换为笛卡尔下的表示为
$\begin{array}{l}$
x=sin\theta cos\phi = sin(\frac{1}{2}arccos(1-2\xi)))cos2\pi\psi \\
y=sin\theta sin\phi = sin(\frac{1}{2}arccos(1-2\xi)))sin2\pi\psi\
z=cos\theta = cos(\frac{1}{2}arccos(1-2\xi))
\end{array}

PBRT中给出了另一种计算办法，将均匀分布在圆盘上的点投影到半球上，其结果就满足Cosine-Weighted。

以下给出证明

假定在圆盘上的极坐标分布为$p(r, \phi)=\frac{r}{\pi}$（使用$\phi$方便后续将$r$对应为$\theta$相关），$p(r, \phi)=\frac{p(\theta, \phi)}{\vert J_t(r, \theta)\vert}$

$\begin{array}{c}r=sin\theta =T_1\left(r\right)\\ \varphi =\varphi =T_2\left(\varphi \right)\end{array}$
\begin{array}{l}
r=sin\theta = T_1(r) \\
\phi=\phi = T_2(\phi)
\end{array}

$J_t(r, \theta)=\left[$
\begin{matrix}
cos\theta & 0 \\
0 & 1 \\
\end{matrix}
\right] = cos\theta

即有$p(\theta, \phi)=cos\theta p(r, \phi)=\frac{r cos\theta}{\pi} = \frac{sin\theta cos\theta}{\pi}$，和上述中得到的结果一样。

下图为两种方法产生的Cosine-Weighted对比

三角形均匀采样

PBRT中采用了等腰切两边为1的三角形特殊情况，不过以下计算办法可以变换回任何三角形

有$p(u,v)=2$（面积倒数），则有

$\begin{array}{c}p\left(u\right)={\int }_0^{1-u}p(u,v)dv=2-2u,p\left(v\mathrm{\mid }u\right)=\frac{p(u,v)}{p\left(u\right)}=\frac{1}{1-u}\\ P\left(u\right)={\int }_0^{u}p\left(u\right)du=2u-u^2,P\left(v\mathrm{\mid }u\right)={\int }_0^{v}p\left(v\mathrm{\mid }u\right)dv=\frac{v}{1-u}\end{array}$
\begin{array}{l}
p(u)=\int_{0}^{1-u}p(u,v)dv=2-2u, \quad p(v\vert u)=\frac{p(u,v)}{p(u)}=\frac{1}{1-u} \\
P(u)=\int_{0}^{u}p(u)du=2u-u^2, \quad P(v\vert u)=\int_{0}^{v}p(v\vert u)dv=\frac{v}{1-u}
\end{array}

这里反变换CDF开根号时要注意到$u,v\in [0,1]$

因此有$u=1-\sqrt{\xi},v=\sqrt{\xi}\psi$

下图中即为三角形上的均匀采样

根据二维分段函数分布采样

这里分段函数的采样即为离散随机变量，若有横向纵向各$n_u,n_v$个元素，函数上指定位置一点值为$f(u,v)$，那么就有

$\begin{array}{c}{I}_f={\int }_v{\int }_{u}f(u,v)dudv=\frac{1}{n_u{n}_v}{\sum }_{i=0}^{n_u-1}{\sum }_{j=0}^{n_v-1}f(u_i,v_j)\\ p(u,v)=\frac{f(u,v)}{I_f}\end{array}$
\begin{array}{c}
I_f=\int_v \int_u f(u,v)dudv=\frac{1}{n_un_v}\sum_{i=0}^{n_u-1}\sum_{j=0}^{n_v-1}f(u_i,v_j) \\
p(u,v)=\frac{f(u,v)}{I_f}
\end{array}

而边缘概率密度可直接得到
$p(u)=\int_v p(u,v)dv=\frac{\frac{1}{n_u}\sum_i f(u, v_i)}{I_f} , \quad p(v\vert u)=\frac{p(u,v)}{p(u)}=\frac{f(u,v)}{\frac{1}{n_u}\sum_i f(u, v_i)}$

之后利用CDF反变换，即PBRT中distribution1d的实现办法可完成对于$p(u),p(v\vert u)$上的采样

此处效果可见前文中的二维分段函数采样的结果

圆锥均匀采样

类似于球上的均匀采样, 易证随机变量$\theta, \phi$相互独立

已知$p(\omega)=\frac{1}{2\pi(1-cos\theta_{max})}$，则$p(\theta, \phi)=\frac{sin\theta}{2\pi(1-cos\theta_{max})}$

$p(\theta)=\int_{0}^{2\pi}p(\theta, \phi)d\phi=\frac{sin\theta}{1-cos\theta_{max}}, \quad p(\phi)=\int_{0}^{2\pi}\frac{sin\theta}{2\pi(1-cos\theta_{max})}d\theta=\frac{1}{2\pi}$

$P(\theta)=\int_{0}^{\theta}\frac{sin\theta}{1-cos\theta_{max}}d\theta=\frac{1-cos\theta}{1-cos\theta_{max}}, \quad P(\phi)=\int_{0}^{\phi}\frac{1}{2\pi}d\phi=\frac{\phi}{2\pi}$

若有两随机变量$xi, \psi$，运用反变换可有（此处省略了$\theta, \phi$到笛卡尔的转换）

$cos\theta=1-\xi +\xi cos\theta_{max}, \quad \phi=2\pi\psi$

下图中即为圆锥上的均匀采样

关于连续型随机变量的分布转换，除了使用反CDF函数将均匀分布函数转换为其他分布函数以外，存在一种通用办法实现不同分布之间的转换，不只局限于均匀分布。

假定存在随机变量$X$，其累积分布函数为$F_X(x)$。若存在单调函数$g$，使得$Y=g(X)$（因为是单调函数，因此$X$与$Y$的关系为单射），则为了计算$Y$的累积分布函数$F_Y(y)$，

设$g(x)$此时为严格单调递增

$\begin{array}{ccc}{F}_Y\left(y\right)& =& Pr\{Y⩽y\}\\ & =& Pr\left\{g\right(X)⩽y\}\\ & =& Pr\{X⩽g^{-1}(y\left)\right\}\\ & =& F_X\left(g^{-1}\right(y\left)\right)\end{array}$
\begin{array}{l}
F_Y(y) & = & Pr\{ Y\leqslant y \} \\
& = & Pr\{g(X)\leqslant y\} \\
& = & Pr\{ X\leqslant g^{-1}(y) \} \\
& = & F_X(g^{-1}(y))
\end{array}

此时对终式左右对x求导(累积分布函数导数为概率密度函数)

$\begin{array}{c}{f}_Y\left(y\right)\frac{dy}{dx}=f_X\left(g^{-1}\right(y\left)\right)\\ f_Y\left(y\right)=\left(\frac{dy}{dx}{)}^{-1}{f}_X\right(g^{-1}\left(y\right))\end{array}$
\begin{array}{l}
f_Y(y)\frac{dy}{dx}=f_X(g^{-1}(y)) \\
f_Y(y) = (\frac{dy}{dx})^{-1}f_X(g^{-1}(y)) \\
\end{array}

再设$g(x)$此时为严格单调递减

$\begin{array}{ccc}{F}_Y\left(y\right)& =& Pr\{Y⩽y\}\\ & =& Pr\left\{g\right(X)⩽y\}\\ & =& 1-Pr\{X⩽g^{-1}(y\left)\right\}\\ & =& 1-F_X\left(g^{-1}\right(y\left)\right)\end{array}$
\begin{array}{l}
F_Y(y) & = & Pr\{ Y\leqslant y \} \\
& = & Pr\{g(X)\leqslant y\} \\
& = & 1 - Pr\{ X\leqslant g^{-1}(y) \} \\
& = & 1 - F_X(g^{-1}(y))
\end{array}

同样的有
$f_Y(y) = -(\frac{dy}{dx})^{-1}f_X(g^{-1}(y))$

则有$f_Y(y) = \vert (\frac{dy}{dx})^{-1} \vert f_X(g^{-1}(y))$。

PBRT中讲到，当我们有一概率密度为$p_x(x)$的随机变量$X$，想要转换为满足已知分布为$p_y(y)$的随机变量$Y$，那么即有下式成立(此过程与上式正好相反)

$\begin{array}{ccc}{F}_X\left(x\right)& =& Pr\{X⩽x\}\\ & =& Pr\left\{g\right(X)⩽g(x\left)\right\}\\ & =& Pr\{Y⩽g(x\left)\right\}\\ & =& F_Y\left(g\right(x\left)\right)\end{array}$
\begin{array}{l}
F_X(x) & = & Pr\{ X\leqslant x \} \\
& = & Pr\{g(X)\leqslant g(x)\} \\
& = & Pr\{ Y\leqslant g(x) \} \\
& = & F_Y(g(x))
\end{array}

$g(x) = F_Y^{-1}(F_X(x))$或当$g(X)$为单调减函数时$g(x) = F_Y^{-1}(1 - F_X(x))$，PBRT中未对此处进行详细说明。

因此当$X$为满足$[0, 1]$区间均匀分布的随机变量时，$F_X(x)=x$，那么上式中$F_X(x))$或是$1 - F_X(x)$都满足$[0, 1]$区间均匀分布，则$g(x)=F_Y^{-1}(x)$，即Inverse Transform Sampling得证。

多维随机变量的转换$T(x)$为双射变换，则满足$f_Y(y)=f_Y(T(x))=\frac{f_X(x)}{\vert J_T(x)\vert }$，且$T(x)=(T_1(x),\cdots T_n(x))$

$J_T(x)=\left[$
\begin{matrix}
\frac{\partial T_1}{\partial x_1} & \cdots & \frac{\partial T_1}{\partial x_n} \\
\vdots & \ddots & \vdots \\
\frac{\partial T_n}{\partial x_1} & \cdots & \frac{\partial T_n}{\partial x_n} \\
\end{matrix}
\right]

蒙特卡洛方法求积分以及部分所需的概率论术语可以在PBRT以及概率论与数理统计中找到

PBRT中给出了蒙特卡洛估计量，其中随机变量$X_i \in [a,b]$且独立同分布，分布满足概率密度函数 $p(x)$。

$F_N = \frac{1}{N}\sum^{N}_{i=1}\frac{f(X_i)}{p(X_i)}$

其期望为

$\begin{array}{l}$
E[F_N] & = E[\frac{1}{N}\sum_{i=1}^{N}\frac{f(X_i)}{p(X_i)}] \\
& = \frac{1}{N}\sum_{i=1}^{N}\int_{a}^{b}\frac{f(x)}{p(x)}p(x)dx \\
& = \frac{1}{N}\sum_{i=1}^{N}\int_{a}^{b}f(x)dx \\
& = \int_{a}^{b}f(x)dx \\
\end{array}

方差为

$\sigma^2=\frac{1}{N}\int(\frac{f(x)}{p(x)}-I)^2p(x)dx$

结果的误差与标准差成正比，因此随着样本数增加误差缩小速度仅与$\sqrt{N}$相关(即常说的增加4倍采样数目才能缩小一半的误差)

PBRT以及许多其他文章书籍等直接给出了这个估计量的期望计算（其中第二步到第三步并未直接说明来由，尽管PBRT在对期望的简介中已给出式子），这一步只能证明估计量本身无偏*。

以下将给出证明

引用一个知识点: Law of the unconscious statistician，简称LOTUS。用法是已知随机变量X的分布$f_X$，但并不知道函数g(X)的分布$f_{g(X)}$。那么此时函数$g(X)$的期望为

$E[g(X)]=\sum_x g(x)f_X(x)$(X为离散型随机变量)

$E[g(X)]=\int_{-\infty}^{\infty} g(x)f_X(x)dx$(X为连续型随机变量)

此处细节介绍也可以看Wyman的技术博客，其中就提到了许多地方都没有涉及到的LOTUS。

$\begin{array}{l}$
E[ \frac {f(X_{i})}{pdf(X_{i})} ] & = E[ \frac {f(x)}{pdf(x)} ] \\
& = \int _{a}^{b}\frac {f(x)}{pdf(x)}pdf(x)dx \\
& = \int _{a}^{b}f(x)dx
\end{array}

这里积分区间变为$[-\infty, \infty]$也是如此。以下将会使用到大数定律的知识背景。

引用自维基百科：设 $a_{1},a_{2},…,a_{n},…$为相互独立的随机变量，其数学期望为： $E(a_{i})=\mu (i=1,2,…)$，方差为： $Var(a_{i})=\sigma ^{2}(i=1,2,…)$
则序列$\overline{a} = \frac{1}{n} \sum_{i=1}^{n}$，$a_{i}$ 依概率收敛于 $\mu$（即收敛于此数列的数学期望 $E(a_{i})$）。

取一组独立同分布的随机变量$\{\xi\}$，且$\xi$在$[a,b]$内满足分布律$p(x)$，则令$p^$(x)=\frac{f(x)}{p(x)}，**则$\{ p^(\xi_i) \}$也是一组独立同分布的随机变量。**，那么计算其得到的期望其实就是积分本身(见下)。

由大数定理

$Pr(\lim_{N\to\infty}\frac{1}{N}\sum_{i=1}^{N}p^*(\xi_i)=I)=1$

那么这里已经有随机变量$\{ p^$(\xi_i) \}存在，且期望等于积分值，**那么根据大数定理可知，这里的$\{ p^(\xi_i) \}$就是会依概率收敛于积分值。**证毕。