Screen Space Fog of War

战争迷雾本身有着非常多的实现方案，类似Dota这样的MOBA游戏早在WC3中就有迷雾的效果实现。这里介绍一个基于屏幕空间战争迷雾的实现效果。

基于屏幕空间的战争迷雾，其核心是一张2D的ShadowMap，之后只需要在全屏Pass下，利用Depth+ClipSpacePosition来重建世界坐标，再从世界坐标转换到2D阴影贴图的局部坐标系下，即可得到当前像素的阴影值。

float depth = DepthTexture.Sample(positionNDC);
float3 positionWS = float4(float3(positionNDC, depth) * 2.0 - 1.0f, 1.0f);
positionWS = mul(_inverseVP, positionWS);
positionWS.xyz /= positionWS.w;

左图为Depth, 右图为重建出的WorldSpace Position。

因此基于屏幕空间的战争迷雾，最核心的就是计算得到的2D阴影贴图，以下列举的不同方案只是在计算这张阴影贴图的过程有所不同。

Grid

Introduction

网格方案在WC3时代就已经被广泛应用，将地图预计算为一张地图障碍物贴图，CPU根据玩家位置实时填充数据，以计算视野阴影贴图。最后转为GPU可读的RT作为2D Shadow。由于CPU填充能力较低，一般最后会辅以Blur来弥补画面缺陷。

左图为预计算的地图障碍物贴图，中间为当前帧可视范围。这里对象移动过的范围将会被标记为已探索，一般实际游戏会对这块区域做提亮操作，如图中白色部分表示为已知探索范围。

核心的CPU填充算法非常直观，本质就是借助队列实现的四邻域填充算法

queue.Enqueue(rootPixel);
while(queue.Count > 0) {
	current = queue.Dequeue();

	// if rootPixel could see current pixel
	if(RayCast(current, rootPixel)) 
		SetVisible(root);

	// spread the visible area around root position in four direction
	EnqueueAtPosition(root.x - 1, root.y, rootPixels, radius);
	EnqueueAtPosition(root.x, root.y - 1, rootPixels, radius);
	EnqueueAtPosition(root.x + 1, root.y, rootPixels, radius);
	EnqueueAtPosition(root.x, root.y + 1, rootPixels, radius);
}

由于CPU在填充过程中需要等待，因此将数据更新另开线程，则阴影贴图的更新可以延迟于玩家移动，不影响主线程整体运行表现。

为了弥补多线程填充完成带来的突变感，存下当前迷雾帧以及上一帧的数据(Texture中R和B通道)，在渲染时对其进行插值过渡，以避免突兀。

在WC3中，移动到一定距离才会触发迷雾的更新，和上述思路基本类似

网格方案较为流行也容易实现，但由于CPU填充能力有限，即便是能做到仅对脏区域局部更新，CPU仍然对高分辨率的需求无法得到较好的满足，且最后一般都需要提供较为高昂的Blur来模糊分辨率带来的界限。不过由于迷雾的特性，低分辨率有时反倒在边缘上能带来更好的过渡感。

Reference

游戏中的战争迷雾

【Unity】FOV战争迷雾

unity下一种基于渲染可见区域的战争迷雾

Signed Distance Field Shadow

Introduction

SDF方案对CPU最为友好，几乎所有计算都可以在GPU中完成。若为静态场景可预bake场景成一张障碍物贴图，动态场景可使用正交投影相机在上方正交拍摄Depth再转换得到。之后使用SDF生成算法对这张障碍物贴图计算Min Signed Distance。最后对这张SDF进行RayMarching来得到一张2D阴影贴图。

从左至右依次为场景Map的障碍物信息，计算得到的SDF贴图，以及最终的2D阴影贴图。

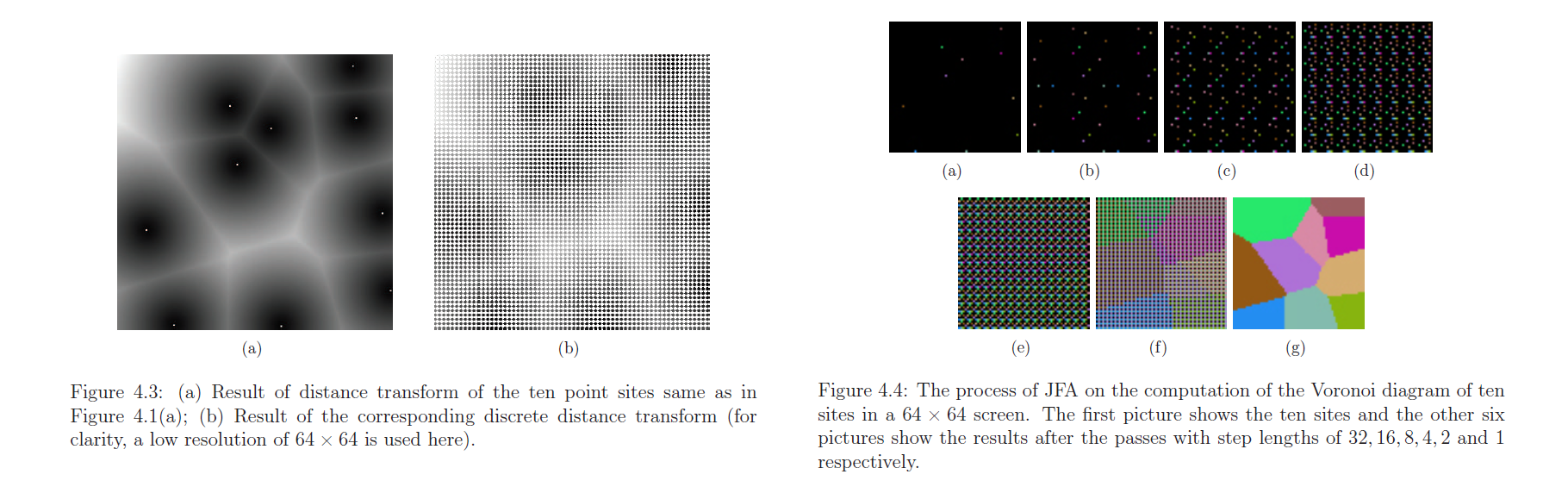
本文选用JFA算法($Reference^{[1]}$)来实时更新SDF贴图。其支持GPU并行，且复杂度仅为O(Nlogn)。要求是Texture的分辨率需要为2的幂次方。

链接为作者描述JFA的Phd论文，也可以查看Jump Flooding in GPU with Applications to Voronoi Diagram and Distance Transform，但上面这篇在错误分析和变种应用上讲解的更为详尽。

SDF生成算法有较多种，可以参考$^{[2]}$中第五章中提供的几种经典算法来生成SDF贴图

JFA的具体思路就是，将复杂的待计算的格点p到3D表面或者2D形状边缘的距离，转化多Pass下，每个Pass中p找到八邻域3D/2D坐标于Seed的距离。其选择的八邻域到p的距离Step，将会不断除2直至为1(logN/2, logN/4, … 16, 8, 4, 2, 1)后得到最终的SDF Texture。

float power = Math.Log2(textureWidth);
for(int i = 0; i <= power; i++) {
	int index0 = i % 2;
	int index1 = (i + 1) % 2;
	
	mat.SetFloat("_Power", power);
	mat.SetFloat("_Level", i);
	mat.SetTexture("_SDFTexture", pingpong[index0]);

	Blit(mat, pingpong[index1]);
}

float stepwidth = _Power - _Level + 1;

for (int y = -1; y <= 1; ++y) {
	for (int x = -1; x <= 1; ++x) {
		// Sample semi-finished sdf texture
		float2 uv = texCoord + float2(x, y) * _TexelSize * stepwidth;
		float4 value = Sample(_SDFTexture, uv);
		float2 seedCoord  = value.zw;
 
		float distance = length(texCoord - seedCoord);
		if ((seedCoord.x != 0.0 || seedCoord.y != 0.0) && distance < minDistance) {
			minDistance = distance;
			minCoord    = seedCoord;
        }
    }
}

JFA本身是存在一定error的，但作者在文章中对不同场景提出了几个算法上的变种(JFA2, 1+JFA…)用于减少Error。上述Phd论文中还分享了在Voronoi Diagram，Delaunay Triangulation, Direct Shadow等应用的原理

计算2D Shadow中的Sphere RayMarching本身很好理解，将SDF图中采样的值，也就是到边界的最近距离作为步进的最长距离(步进更大的距离将可能与已有边界碰撞)。

float drawShadow(float2 uv, float2 lightPos)
{
    float2 direction = normalize(lightPos - uv);
    float2 p = uv;
    float distanceToLight = length(uv - lightPos);
    float distance = 0.0f;

    for(int i = 0; i < 32; i++) {
        float s = Sample(_SDFTexture, p);

        if(s <= 0.00001) return 0.0;
        if(distance > distanceToLight) return 1.0;

        distance += max(s * _StepScale, _StepMinValue);
        p = uv + direction * distance;
    }

    return 0.0;
}

SDF本身是可以直接计算出半影的，但在边界上存在较为严重的BandingArtifact，各类文献报告中均有对此进行改善缓解，一般会选用混合方案来避免这样的问题。其中也有改进后的ConeTracing方法，在UE4以及$Reference^{[2]}$中有过提及。

左图为SDF直接计算得到的半影，右图则为在边界上RayMarching带来的精度不够导致的BandingArtifact现象

演示中为了避免BandingArtifact，并没有直接算出半影而是算出二值图最后配合Blur，并按距离增大Blur半径来模拟半影的效果。

Reference

Jump Flooding in GPU with Applications to Voronoi Diagram and Distance Transform

Signed Distance Fields in Real-Time Rendering

Chapter 30. Real-Time Simulation and Rendering of 3D Fluids

Jump Flood Algorithm: Points

Jump Flood Algorithm: Shapes

2d signed distance functions

Mesh Projetion

Introduction

2D阴影由于其特殊性，可以由CPU直接计算出一个变形后的Mesh作为平面的阴影区域。

这里需要对障碍物进行边缘编辑，以调整出适应形状的阴影区域

对场景中所有变形后的Mesh，多次的渲染到一张RT上，即可得到所需的2D Shadow Map(本方法在Demo中并未涵盖，可参考Asset Store的SFSS插件)

若是场景中物体较多，则计算阴影区域的CPU压力将会较大，且即便为静态场景可能也需要多次的DrawMesh才能得到最后的2D ShadowMap。但其优势是在Shader中较前两者，可以较好的控制半影区域的绘制，以得到高质量的阴影结果。

Reference

Unity Asset Store: SF Soft Shadow 2D

Summary

由于实现战争迷雾的方案较多，这里仅提供一个Unity上的基于屏幕空间战争迷雾的提供了上述Grid和SDF方案实现的项目Fog of War以供参考(Mesh Projetion的方案可以直接使用Unity SFSS的插件)

Demo中SDF可使用较高分辨率来完成实时预览一般给定128x128或者256x256皆可(过高分辨率需要更多次的Blur来带来半影的效果)。

而CPU的填充版本则由于C填充性能有限，因此建议给定64 x 64或32 x 32获得更平滑的效果。

Introduction

离线渲染中，对于面积光的渲染也有较多研究，多为在面积光源形状上做采样，配合BRDF进行MIS，但这在实时渲染中要想收敛则采样数过多开销过大。

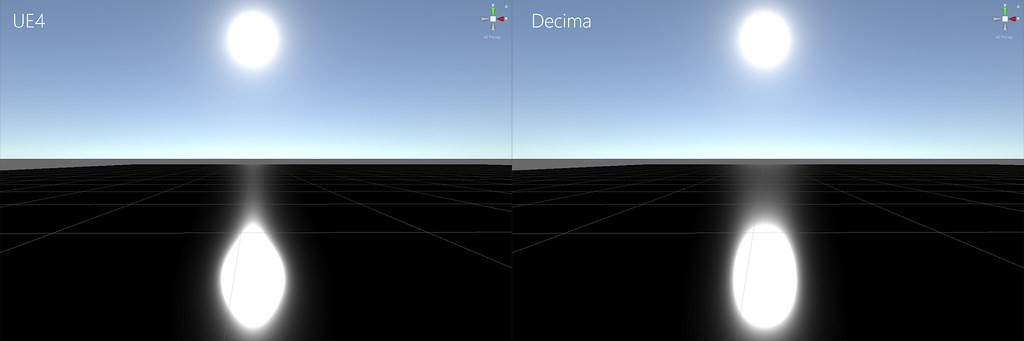
Eric Heitz$^{[5]}$曾对多边形的实时面积光渲染做出较好的模拟，对球面积光的近似多采用Karis$^{[2]}$在13年发布的Representative Point Method，其实现较为高效又兼容GGX微表面被广泛采纳。Decima在Siggraph 2017$^{[1]}​$上又对其进行了改进，使其在边缘处拖尾更接近Reference(如图)。

但无论是UE4或是Decima都无法保证Physically Based，也就是不满足Energy Conservation，仅能实现较为近似的效果。因此这里不对Normalization Factor做过多记录。

Decima: We’re currently experimenting with alternative formulas for
normalization to better match our reference. This, however, is still in flux.

UnrealEngine: To derive an approximate normalization for the
representative point operation we divide the new widened normalization factor by the original

Representative Point Method

Unreal Engine 4

Representative Point的核心思想就是使用一个点来模拟一个球面光的效果。在GGX BRDF计算中，光照方向不再固定，而是来自于球面，因此关键是如何确定光照方向。

// no more punctual light direction
float3 L = normalize(lightPoint - hitPoint);
// but get L from spherical area light
float3 L = getLightDirection(normalize(lightPoint - hitPoint), ...);

需要注意的是，此方法对平行光同样有效(平行光本为点光无限远的近似)，仅需将原始L改为平行光方向即可。

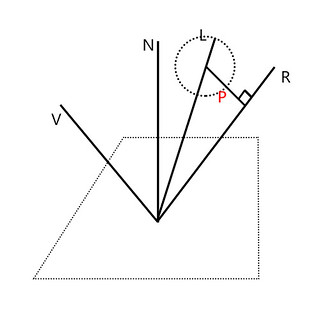
Karis提出的解决上述问题的核心思想是，当反射光向量R与球相交，则此时R就是光照方向向量。R处于球外时，若为离线渲染中，则此时应在球面上大量采样来求解对表面BRDF的贡献。由于为实时渲染，思路就是选取对表面光照贡献最大的点作为光照方向。此时选择球面上离反射向量R最近的点作为光照来源(如图)。

float3 getLightDirection(float3 L, float3 R, float radius)
{
	float3 centerToRay = R * dot(L, R) - L;
	// ray intersected / not intersected both combined(saturate)
	float3 closestPoint = L + centerToRay * saturate(radius / length(centerToRay));
	// the length of closestPoint could be used for normalization
	return normalize(closestPoint);
}

上述UE4实现中，已经包含了反射光与球相交/不想交的情况。因此仅需对GGX的光照来源进行改变即可快速模拟球面光。

UE4中的近似Normalization Factor选择如下，由于仅为近似解，因此PDF中也未包含详细推导

$\alpha=roughness^2$

$\alpha' = saturate(\alpha+\frac{sourceRadius}{3*distance})$

$normalizationFactor=(\frac{\alpha}{\alpha'})^2$

Decima

Decima的近似实现也沿用了UE4的方法，变化的是选取光照来源位置不再是反射光线最近的点，而是能使得$N \cdot H$最大的点(GGX高光分布中N与H越接近，或者说R与L越接近则起光照在BRDF上的贡献最大，可自行查看Disney BRDF Explorer中GGX的分布)。

Decima采取如下方式选取光照方向

$T=\frac{R - (L \cdot R) * L}{\| R - (L \cdot R) * L \|}$

$L = \sqrt{1 - s^2}*L_c+s*T$

这里有一处微调，不再是向R投影，而是投影至Lc(如图)

取$B, L_c, T$为一坐标系，在此圆盘上找到一个$\phi$，使得$N \cdot H$达到最大的点。

$B=T \times L_c$

$L=\sqrt{1 - s^2}L_c+s*(\cos{\phi} * T + \sin{\phi} * B)$

由于$tan{\frac{\phi}{2}}$可以万能表示$\sin{\phi}$， $\cos{\phi}$，且在区间内单调递增，因此将求取$\phi$转为求$x=tan{\frac{\phi}{2}}$。且令$f(x)=(N \cdot H)^2$(选此因为分式上含根号，且可直接将$(N \cdot H)^2$用于GGX的NDF计算上)

$f(x)=\frac{ax^4+bx^3+cx^2+dx^2+e}{gx^4+hx^3+ix^2+jx^2+k}, x=tan{\frac{\phi}{2}}$

此处推导过于繁琐，因此未给出具体展开式

取$x_0=0,f(x_0)=Karis's (N\cdot H)^2$

由于牛顿迭代可求函数根，对$x_{n+1}=x_n-\frac{f(x_n)}{f'(x_n)}$做多次迭代则可收敛至根值。此时要求$f(x)$最大值，因此对$x=f(x)$进行牛顿迭代，则根值处为$f'(x)=0$求得最大值。取$f(x_1)$为最终结果。

$x_{n+1}=x_n-\frac{f'(x_n)}{f''(x_n)}$

float GetNoHSquared(float radiusTan, float NdotL, float NdotV, float VdotL)
{
	// See presentation for more deatil
}

void EvaluateNdotH(float radius, float roughness, float lightCenterDistance, float NdotL,float NdotV, float LdotV, inout float NdotH)
{
	float radiusTan = max(0.001, radius / lightCenterDistance - roughness * 0.25);
    NdotH = sqrt(GetNoHSquared(radiusTan, NdotL, NdotV, LdotV));
}

void EvaluateNormalizationFactor(float roughness, float LdotH, float radius)
{
	// Decima: Still in flux
	float roughnessSquaredLdotH = roughness * roughness * (LdotH + 0.001);
    normalization = roughnessSquaredLdotH / (roughnessSquaredLdotH + 0.25 * radius * (2.0 * roughness + radius));
}

这里使用时，需格外注意提供给GGX计算的，除更改后的NdotH外，NdotL, NdotV, VdotL, LdotH中的L与H皆为初始$L=normalize(point-hitPoint)$方向，尽管这样会在Point垂直于Normal时失效，但仍然能取得较好的效果

ScreenShots

下图为Unity 2018中实现对比结果，可明显看见接近边缘处的拖尾更接近Reference，也就可以实现地平线中夕阳的拖尾效果。

Reference

1. Decima Advances in Lighting and AA
2. Real Shading in Unreal Engine 4
3. A Reflectance Model for Computer Graphics
4. Microfacet Models for Refraction through Rough Surfaces
5. Real-Time Polygonal-Light Shading with Linearly Transformed Cosines

Introduction

本文基本理论及其实现参考GPU Gems 2$^{[1]}$和Scratchapixel$^{[2]}$

大气的效果主要是由大小的粒子经过大量散射后带来的结果。 其中光被分子大小的粒子散射称之为Rayleigh scattering，而更大一些的沙尘散射被称之为Mie scattering。 大气散射的结果主要是由这两部分组成。 本文未实现多重散射，以及点光源等更通用的方法，而是使用单级散射配合上平行光的结果。

Out-Scattering And In-Scattering

Out-Scattering

In-Scattering

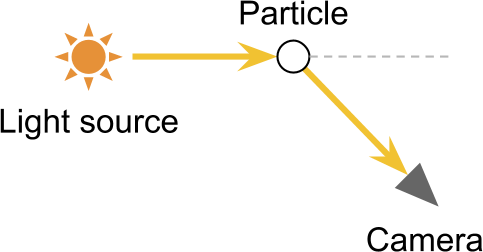
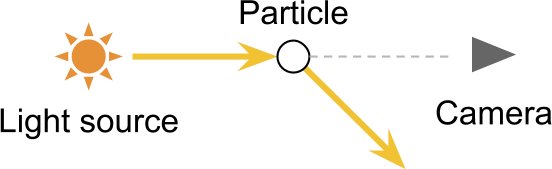
如若有一平行光(这里假定太阳无限远，则光源近似于平行光)入射大气相交C点，则由于Out-Scattering的影响光照强度将会有一定衰减，其中T为衰减系数。

$I_P = I_C \cdot T(\overrightarrow{CP})$

从P点的光照抵达A点时，会发生由P点的大气粒子经过散射造成的In-Scattering，从$\overrightarrow{CP}$方向变为$\overrightarrow{PA}$方向，散射系数定义为S，$\lambda$为光的波长，$\theta$为散射角度，$h$为相对海拔高度。 同样也会由于在路径$\overrightarrow{PA}$上造成衰减。

$I_A=I_P \cdot S(\lambda, \theta, h) \cdot T(\overrightarrow{PA})$

S表示的是在某一方向上的散射系数，以Rayleigh scattering为例

$S(\lambda, \theta, h)=\frac{\pi^2(n^2-1)^2}{2} \frac{\rho(h)}{N} \frac{1}{\lambda^4}(1+cos^2\theta)$

其中$S(\lambda, \theta, h)$可以拆分为三项，$P(\theta)$就是体渲染中常见的Phase Function

$S(\lambda, \theta, h)=\beta(\lambda,h)P(\theta)=\beta(\lambda)\rho(h)P(\theta)$

无论是Mie还是Rayleigh其大气密度都随着海拔接近于指数下降

$\rho(h)=e^{-\frac{h}{H}}$

Rayleigh Scattering And Mie Scattering

这里$\beta(\lambda,h)$可以通过对$S(\lambda, \theta, h)$在整个球面上进行积分，以算出在总方向上的散射系数。 其中可以预计算完$\beta=(33.1e^{-6}, 13.5e^{-6}, 5.8e^{-6})m^{-1}$

$\begin{array}{l} \beta(\lambda, h)_{Rayleigh} &=& \int^{2\pi}_{0}\int^{\pi}_{0}S(\lambda, \theta, h)sin\theta d\theta d\phi\\[2ex] &=& \frac{\pi^2(n^2-1)^2}{2} \frac{\rho(h)}{N} \frac{1}{\lambda^4} \int^{2\pi}_{0}\int^{\pi}_{0}(1+cos^2\theta)sin\theta d\theta d\phi\\[2ex] &=& \frac{8\pi^3(n^2-1)^2}{2} \frac{\rho(h)}{N} \frac{1}{\lambda^4} \end{array}$

大气中的吸收系数可以忽略不计，因此散射系数基本由Phase Function决定。 其对应的Phase Fucntion为

$\begin{array}{l} P(h) & = & \frac{S(\lambda, \theta, h)}{\beta(\lambda)} \\[2ex] & = & \frac{3}{16\pi} (1+cos^2\theta) \end{array}$

Mie Scattering不像Rayleigh那样，其大小变化也接近于从海拔1位置处指数下降，这里取$\beta(\lambda, 0)=210e^{-5}m^{-1}$，$g = 0.76$

$\beta(\lambda, h)_{Mie}=\beta(\lambda, 0) \cdot e^{-\frac{h}{H_M}}$

$P(h) = \frac{3}{8\pi} \frac{(1-g^2)(1+cos^2\theta)}{(2+g^2)(1+g^2-2gcos^2\theta)^{\frac{3}{2}}}, g \in (-1, 1)$

Optical Depth

衰减指数T与海拔高度有关，非定值，因此需要在海拔上做积分

$T(\overrightarrow{PA})=e^{-\int^A_P \beta(\lambda, h)ds}=e^{-\beta(\lambda)\int^A_P \rho(h)ds}$

此处令光学深度D为

$D(\overrightarrow{PA})=\int^A_P \rho(h)ds$

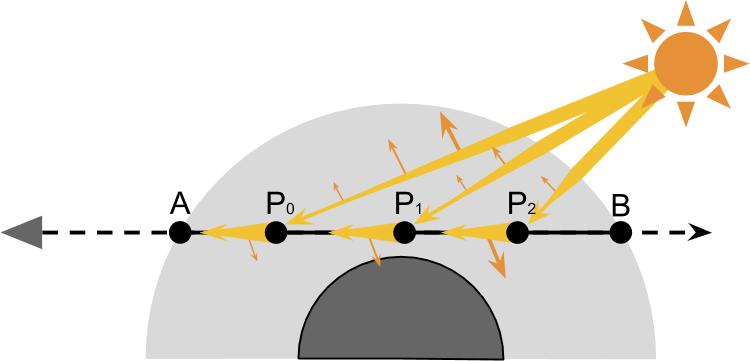
则最终进入到A处的光照为

$\begin{array}{l} I_A &=& \int^B_A I_{P} \cdot S(\lambda, \theta, h) \cdot T(\overrightarrow{PA}) d\\[2ex] &=& \int^B_A I_{C} \cdot T(\overrightarrow{CP}) \cdot S(\lambda, \theta, h) \cdot T(\overrightarrow{PA}) ds\\[2ex] &=& I_{C} \cdot \beta(\lambda) \cdot \rho(h)\int^B_A e^{-\beta(\lambda)(D(\overrightarrow{CP}) + D(\overrightarrow{PA}))} \cdot \rho(h) ds \end{array}$

Implementation

RayMarching

这里借鉴英伟达Demo，利用vs来生成一个全屏的三角形$^{[10]}$，以方便在PS中RayMarching(因为在VS中无需任何输入)。 此处由于使用了真实的物理数值，因此在Shader实现中需要注意float会溢出的问题，可以通过暂存为double或做单位转换来解决

具体实现可参考Sophia渲染器中shader/skyRayCasting/部分

// vs 
struct output{ // something 
};

output main(uint id : SV_VertexID)
{
    output o;

    o.texCoord = float2((id << 1) & 2, id & 2);
    o.position = float4(o.texCoord * float2(2, -2) + float2(-1, 1), 0, 1);

    return o;
}

// ps
// do some ray march stuff

Mesh Based

这一部分其基本原理与上述是一致的，主要参考于GPU Gems 2$^{[1]}$。 不同之处在于，Sean O’Neil提出了一个将大气预计算到LUT的方式，具体实现可以参考Sophia渲染器中shader/sky/部分

共计四张纹理，其中光学深度为HDR(部分会超过1)。 密度LUT中x表示海拔(映射为(0, 1))高度，y表示垂直角度(0时笔直朝上，1垂直向下)。 RGBA中Rayleigh与Mie各占一半，Rayleigh部分的密度以及Depth如下图

实现可以参考test中的earth的MakeOpticalDepthBuffer函数

Result

RayMarching结果较好，无论是在太空中或者是球内都有较为不错的结果

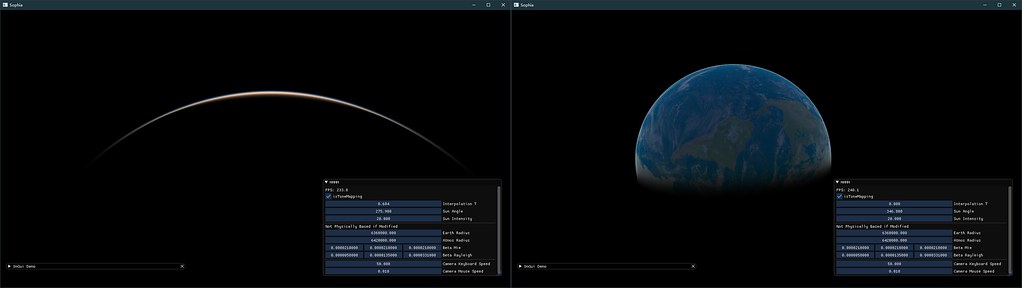
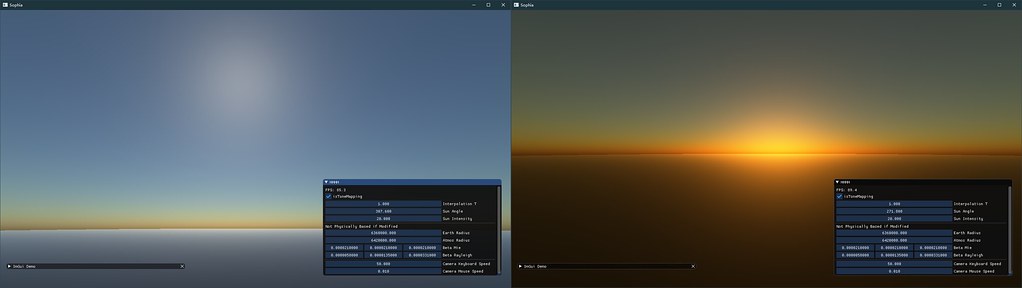
Mesh Based远观效果是可以的，这里的球生成的时候只有64*64的细分程度，再配合上LUT，帧率能跑到1000+fps。 但其缺点是不可近看，在低面数下插值涂抹感比较严重，除非将球的面数成倍的增加，这样就带来了带宽和计算压力显得不是很必要(这里借鉴GPU Gems没有使用地球大小的参数，因此样式略微不同)

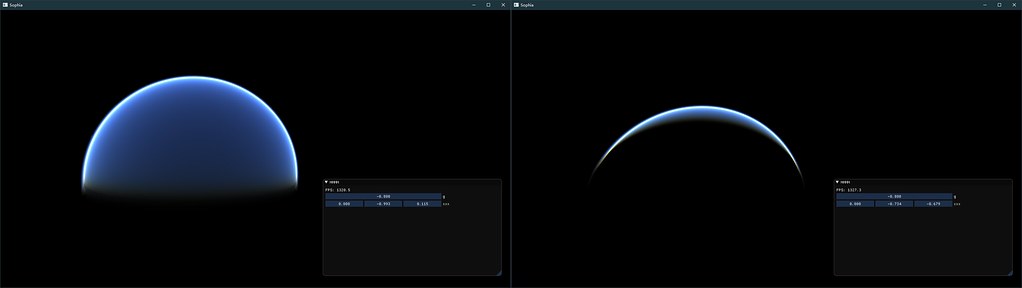
因此最佳的方式应该是，RayMarching+LUT的实现方式(将在未来更新)。 原本做Mesh Based是希望能够将地面一次性也做displacement，不过由于效果一般，因此也没有做球内视角。

Reference

1. GPU Gems 2: Accurate Atmospheric Scattering：基于Mesh的大气渲染模拟实现参考
2. Simulating the Colors of the Sky：基本大气渲染理论推导参考
3. Natural Earth III：地球纹理
4. Practical Implementation of Light Scattering Effects Using Epipolar Sampling and 1D Min/Max Binary Trees
5. Volumetric Atmospheric Scattering：大气理论推导及Shader实现参考
6. Flexible Physical Accurate Atmosphere Scattering：预计算LUT对照参考
7. 基于物理的大气渲染
8. Display of the Earth Taking into Account Atmospheric Scattering
9. Rendering Parametrizable Planetary Atmospheres with Multiple Scattering in Real-Time：93年 Nishita关于大气渲染的推导
10. Vertex Shader Tricks：VS生成全屏Quad做单像素PS的解释

Introduction

本文建立在CodingLabs以及LearnOpenGL$^{[2]}$中介绍的基本PBR概念上。

PBR自身概念不陌生，使用满足基于物理的BRDF，满足能量守恒即可。IBL$^{[6]}$的效果能大大提高观感。 这里选用Cook-Torrance BRDF$^{[7]}$

漫反射部分可选用Lambertian或Oren Nyar BRDF

$f_r=k_d f_{lambert}+ksf_{cook-torrance}$

Cook-Torrance的高光部分如下，公式具体含义可见$^{[8]}$

$f_{cook-torrance}=\frac{DFG}{4(w_o \cdot n)(w_i \cdot n)}$

Normal Distribution Function, Geometry, Fresnel三部分各自选用Trowbridge-Reitz GGX，Schlick-GGX， Fresnel-Schlick approximation(离线也常用Schlick的近似菲涅尔来代替繁重计算)

Cook-Torrance的DFG部分有很多实现，GGX拖尾效果较好，其他部分可参考$^{[5]}$

$N_{GGX}(n,h,\alpha)=\frac{\alpha^2}{\pi((n \cdot h)^2(\alpha^2 - 1)+1)^2$
}

$G_{SchilickGGX}(n,v,k)=\frac{n \cdot v}{(n \cdot v)(1-k)+k}$

$F_{Schilick}(h,v,F_0)=F_0+(1-F_o)(1-(h \cdot v))^5$

其中法线分布中的$\alpha$表示表面粗糙度。 几何项中的k根据direct lighting与IBL选用不同粗糙度映射方式$k_{direct}=\frac{(\alpha+1)^2}{8}, k_{IBL}=\frac{\alpha^2}{2}$。 最后使用光照与视线方向的G相乘$G(n,v,l,k)=G_{sub}(n,v,k)G_{sub}(n,v,k)$

菲涅尔反射计算中的$F_0$可以根据下表查找所得

最后渲染方程($k_s$由菲涅尔给出)

$L_o(p,\omega_o) = \int\limits_{\Omega} (k_d\frac{c}{\pi} + k_s\frac{DFG}{4(\omega_o \cdot n)(\omega_i \cdot n)}) L_i(p,\omega_i)(n \cdot \omega_i) d\omega_i$

Precomputed LUT

贴图选用HDR图像文件，免费HDR文件可从sIBL archive下载

将上述渲染方程左右拆开各做预计算，其中左边为漫反射部分

$L_o(p,\omega_o) = k_d\frac{c}{\pi} \int\limits_{\Omega} L_i(p,\omega_i) n \cdot \omega_i d\omega_i$

转立体角为球坐标系下
$L_o(p,\theta_o,\phi_o) = \frac{c}{ \pi } \int\limits_{\Phi} \int\limits_{\Theta} L_i(p,\theta_i,\phi_i) cos(\theta_i) sin(\theta_i) d\theta_i d\phi_i$

这里使用Monte Carlo Estimator将二重积分转为离散采样($\frac{b-a}{N} \sum_{}^{N} f(x_i)$)，这里采用Uniform Sampling(可更换为MIS方法更快收敛)

$L_o(p,\theta_o,\phi_o) = \frac{c}{ \pi }\frac{2 \pi}{ N_1 } \frac{\pi}{ 2 N_2 } \sum_{}^{N_1} \sum_{}^{N_2} L_i(p,\theta_i,\phi_i) cos(\theta_i) sin(\theta_i)$

$L_o(p,\theta_o,\phi_o) = \frac{\pi c}{ N_1 N_2 } \sum_{}^{N_1} \sum_{}^{N_2} L_i(p,\theta_i,\phi_i) cos(\theta_i) sin(\theta_i)$

此处LearnOpenGL对于黎曼和的推导有误，可参考CodingLabs中最后的推导过程. LearnOpengl使用GPU进行预计算，这里我采用CPU端保存为HDR文件以方便Debug，实现部分基本知识公式的翻译(可查看Sophia中的precomputedMap.h查看)

for(int i = 0; i < width; i++) {
    for (int j = 0; j < height; j++) {
        float phiT = 2PI * i / width;
        float thetaT = PI * j / height;

        // avoid situations when up = normal
        vec3 up(sin(thetaT) * cos(phiT), cos(thetaT), sin(thetaT) * sin(phiT));
        vec3 right = up.crosse(normal);
        vec3 normal = right.crosse(up);

        vec3 irradiance = 0;
        // diffuse irradiance compute hemisphere
        for (float phi = 0; phi < 2PI; phi += 2PI / samples) {
            for (float theta = 0; theta < PI_DIV2; theta += PI_DIV2 / samples) {
                local = vec3(sin(theta) * cos(phi), cos(theta), sin(theta) * sin(phi));
                world = local.x * right + local.y * up + local.z * N; 

                x = SphericalPhi(world) / 2PI * width, 
                y = SphericalTheta(world) / PI * height;

                irradiance += GetColor(x, y) * cos(theta) * sin(theta);
            }
        }
        SetColor(i, j, PI * irradiance / (samples * samples));
    }
}    

右边高光部分也可以拆分为两部分，其中BRDF与IBL在某一分布下做预计算

$L_o(p,\omega_o) = \int\limits_{\Omega} L_i(p,\omega_i) d\omega_i * \int\limits_{\Omega} f_r(p, \omega_i, \omega_o) (n \cdot \omega_i) d\omega_i$

由于微表面的法线分布选用GGX，因此Importance Sampling的策略与PBRT中建议的一致，都是选择在法线分布上进行重要性采样。 积分拆为数值积分

具体公式详解可以参考UE4$^{[9]}$的PBR报告

$L_o(v) \approx (\frac{1}{N}\sum^{N}_{k=1}L_i(l)) (\frac{1}{N}\sum^N_{k=1}\frac{f_r(l, v) (n \cdot l)}{pdf(l, v)})$

很多地方都没有提到这一点，GGX的法线分布pdf在PBRT$^{[1]}$上有过推导

$pdf=\frac{D(h)(h \cdot n)}{4(l \cdot h)}$

因此代入IS下的pdf后，整体就变得更为简洁

$L_o(v) \approx (\frac{1}{N}\sum^{N}_{k=1}L_i(l)) (\frac{1}{N}\sum^N_{k=1}\frac{GF \cdot (n \cdot h)}{(n \cdot h))(v \cdot n)})$

首先是左半边的Pre-filtering HDR environment map部分。 这里也就是UE4中所说的近似带来误差最大的部分(由于预计算，无法得知R具体为多少)，也就是默认V=R=N，即垂直望去反射光线，法线，视线共线。 根据UE4中的展示，其误差效果仍然能够接受

代码实现部分基本上都是公式的直接翻译

for (int i = 0; i < width; i++){
    for (int j = 0; j < height; j++){
        float phi = 2PI * i / width;
        float theta = PI * j / height;

        vec3 N(sin(theta) * cos(phi), cos(theta), sin(theta) * sin(phi));
        vec3 V = N = R;

        float sumWeight = 0;
        vec3 prefilteredColor = 0;

        for (int s = 0; s < sampleCount; s++) {
            random = hammersley(s, sampleCount);
            H = importanceSampleGGX(random, N, roughness);
            L = (2.0 * V.dot(H) * H - V).getNormalized();

            cosL = max(N.dot(L), 0.0f);
            if (cosL > 0.0) {
                x = SphericalPhi(L) / 2PI * width;
                y = s3SphericalTheta(L) / PI * height;

                // The cos here is because UE4 said
                // "As shown in the code below, we have found weighting by coslk achieves better results"
                prefilteredColor += GetColor(x, y) * cosL;
                sumWeight += cosL;
            }
        }
        SetColor(i, j, prefilteredColor / sumWeight);
    }
}
Write(fileName);

这里使用CPU计算会有一个高亮点的问题，如若采样数不够(Sophia采用OpenMP进行多核计算，即便如此，20000的采样数也需要花费几小时才能完成)，如图是一个高光与周围亮度值差距较大的一张HDR纹理，下图即便是采用了30000的采样数也没能解决，可见一味的提升采样数并不能完全的解决问题。

这里LearnOpenGL在计算prefilteredColor时，不直接从原图上采样，而是选用mipmap进行处理，由于我使用了CPU端计算，且自行实现mipmap间插值较为繁琐，因此选用了采样数较大的没有出现bright bots效果的作为替代。 具体实现可参考LearnOpenGL$^{[2]}$

最后将不同Roughness的结果存到不同mimap level上即可，下图为几张不同粗糙度时的结果。

剩下的右半边BRDF部分，做一定预处理

$\int\limits_{\Omega} f_r(l,v) (n \cdot l) dl = \int\limits_{\Omega} \frac{f_r(l,v)}{F(v, h)} F(v, h) (n \cdot l) dl$

$\int\limits_{\Omega} \frac{f_r(l,v)}{F(v, h)} (F_0 + (1 - F_0){(1 - v \cdot h)}^5) (n \cdot l) dl$

$F_0 \int\limits_{\Omega} \frac{f_r(l, v)}{F(v, h)}(1 - {(1 - v \cdot h)}^5) (n \cdot l) dl$
+
\int\limits_{\Omega} \frac{f_r(l, v)}{F(v, h)} {(1 - v \cdot h)}^5 (n \cdot l) dl

vec3 integrateBRDF(float NoV, float roughness, int samples) {
    // V on XoY plane
    vec3 V(sqrt(1.0f - NoV * NoV), NoV, 0.0f);
    vec3 N = 0;
    float A = 0.0f, B = 0.0f;

    for (int i = 0; i < samples; ++i) {
        vec2 random = hammersley(i, samples);
        vec3 H = importanceSampleGGX(random, N, roughness);
        vec3 L = (2.0 * V.dot(H) * H - V).getNormalized();

        float NoL = max(L.y, 0.0f);
        float NoH = max(H.y, 0.0f);
        float VoH = max(V.dot(H), 0.0f);

        if (NoL > 0.0f) {
            float G = geometrySmith(N, V, L, roughness);
            float GVisibility = (G * VoH) / (NoV * NoH);
            float Fc = pow(1.0f - VoH, 5.0f);

            A += (1.0f - Fc) * GVisibility;
            B += Fc * GVisibility;
        }
    }
    return vec3(A, B, 0.0f) / samples;
}

BRDF预计算结果如下图，横纵坐标分别为$cos\theta_v$与Roughness

Result

最后结果也较为可观，尽管没有indirectLighting部分，但总体效果已经很不错了。

Reference

1. PBRT：基于物理的BRDF及其Importance Sampling理论推导
2. LearnOpenGL：基本PBR概念及其实现
3. Physically Based Shading during Black Ops
4. Klayge：Cook-Torrance BRDF的Importance Sampling PDF推导
5. Specular BRDF Reference
6. Image-Based Lighting
7. Cook-Torrance BRDF
8. Physically Based Rendering - Cook–Torrance
9. Real Shading in Unreal Engine 4：实时PBR实现理论推导及其近似解的解释

MVP矩阵推导

其中Model, View的矩阵部分可根据Local转World坐标系转换得到，可参考龙书5.6.1章节。

透视投影矩阵可以分为$x, y$的投影变换，以及$z$的透视校正
首先$x, y$部分可以根据透视变换的相似三角形推导出，此处$x$部分的FOV令为$\theta$，横纵坐标比aspect令为$r=\frac{w}{h}$。

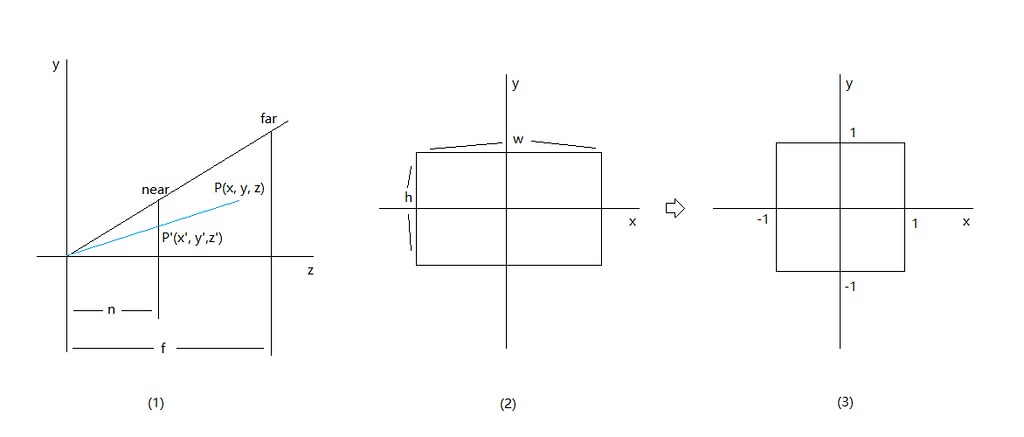
对应$x, y$的转换细节推导可参考透视投影详解

其中$(3)$中的$x'',y''$已经归一化转化到了NDC空间（注意要用$\frac{\theta}{2}$）

$\begin{array}{c}{x}^{\mathrm{\prime }\mathrm{\prime }}=\frac{x}{z}cot\left(\frac{\theta }{2}\right)\frac{1}{r}\\ y^{\mathrm{\prime }\mathrm{\prime }}=\frac{y}{z}cot\left(\frac{\theta }{2}\right)\end{array}$
\begin{array}{l}
x''=\frac{x}{z}cot(\frac{\theta}{2})\frac{1}{r} \\
y''=\frac{y}{z}cot(\frac{\theta}{2})
\end{array}

此时$z$没有做过变换，本质上若需要归一化，也只需要做一个从区间$[n,f]$到$[0,1]$的一个变换即可。但若$z$仅仅只是做了一个区间映射而没有经过透视校正，则会出现下述问题。

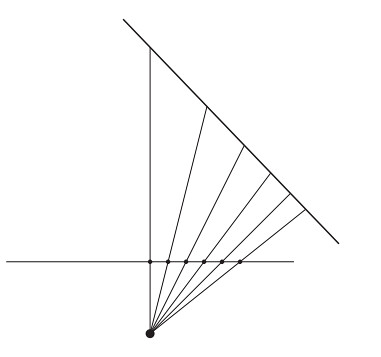
1. Vertex Shader完成顶点变换后需要做光栅化步骤，此时会在投影平面上进行均匀采样。根据上图中，对屏幕上线段进行均匀采样，而其对应线段中的点并非均匀排布。观察发现对应线段上点的$x,y$部分仍然保持均匀分布，但$z$由于透视变换的问题造成结果的畸变。

2. 后续的纹理，颜色插值计算也会因为$z$轴的透视问题带来非均匀分布的问题

本质上的问题是因为$z$在透视变换后，是非线性分布的。因此对应的解决方案就是找到一个能够满足深度前后关系不变，且能支持线性插值的量来代替原有的$z$。

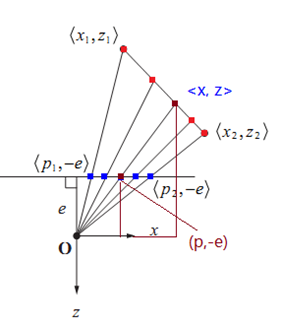
此处证明$\frac{1}{z}$是线性分布的。令直线为$ax+bz=c$，给出线段上一点$[x, z]$，其对应投影平面上的点为$[p, -e]$，即有

$\begin{array}{c}\frac{p}{x}=\frac{-e}{z}\\ (-\frac{ap}{e}+b)z=c\\ \frac{1}{z}=-\frac{ap}{ce}+\frac{b}{c}\end{array}$
\begin{array}{l}
\frac{p}{x} = \frac{-e}{z} \\
(-\frac{ap}{e}+b)z = c \\
\frac{1}{z} = -\frac{ap}{ce}+\frac{b}{c}
\end{array}

设线段的头尾点为$[x_1, z_1], [x_2, z_2]$以及对应投影平面上的点为$[p_1,-e],[p_2,-e]$。令$p_3=(1-t)p_1+tp_2$由$p_1,p_2$线性插值得出，求$[p_3,-e]$对应的线段上的点。

$\begin{array}{ccc}\frac{1}{z_3}& =& -\frac{a{p}_3}{ce}+\frac{b}{c}\\ & =& -\frac{a{p}_1}{ce}(1-t)--\frac{a{p}_2}{ce}t+\frac{b}{c}\\ & =& (-\frac{a{p}_1}{ce}+\frac{b}{c})(1-t)+(-\frac{a{p}_2}{ce}+\frac{b}{c})t\\ & =& \frac{1}{z_1}(1-t)+\frac{1}{z_2}t\end{array}$
\begin{array}{l}
\frac{1}{z_3} & = & -\frac{ap_3}{ce}+\frac{b}{c} \\
& = & -\frac{ap_1}{ce}(1-t)–\frac{ap_2}{ce}t+\frac{b}{c} \\
& = & (-\frac{ap_1}{ce}+\frac{b}{c})(1-t)+(-\frac{ap_2}{ce}+\frac{b}{c})t \\
& = & \frac{1}{z_1}(1-t)+\frac{1}{z_2}t
\end{array}

可见$\frac{1}{z}$在直线上可以线性插值。由于$z$轴在光栅化中需要被插值，因此直接构造$\frac{1}{z}$使得硬件在做插值时保持线性，为了将$z'$归一化到$[0,1]$需要构造$z'=A+\frac{B}{z}+B$。已知

$\begin{array}{ccc}0& =& A+\frac{B}{n}\\ 1& =& A+\frac{B}{f}\end{array}$
\begin{array}{l}
0 & = & A+\frac{B}{n} \\
1 & = & A+\frac{B}{f}
\end{array}

求解方程组，则有$A=\frac{f}{f-n}, B=\frac{nf}{f-n}$

可得最终透视投影矩阵

这里推导的结果为左手系。若左右手系区分则只需要调换部分元素位置，可见龙书推导。

$\left[\begin{array}{cccc}\frac{1}{rtan\left(\frac{\theta }{2}\right)}& 0& 0& 0\\ 0& \frac{1}{tan\left(\frac{\theta }{2}\right)}& 0& 0\\ 0& 0& \frac{f}{f-n}& 1\\ 0& 0& \frac{nf}{f-n}& 0\end{array}\right]$
\left[
\begin{matrix}
\frac{1}{rtan(\frac{\theta}{2})} & 0 & 0 & 0 \
0 & \frac{1}{tan(\frac{\theta}{2})} & 0 & 0 \\
0 & 0 & \frac{f}{f-n} & 1 \\
0 & 0 & \frac{nf}{f-n} & 0
\end{matrix}
\right]

Sophia Renderer上的矩阵

由于DirectX 11的GPU部分采用了列主的矩阵排布。一般有两种解决方案

1. CPU端采用行主，GPU端采用列主，在CPU绑定矩阵到CB的时候转置一次。
2. CPU端采用行主不变，GPU端直接左乘向量(GPU上的矩阵是CPU的转置)

采用两种方式不同的地方在于，前者$MVP=Projection$ View World Vector，后者本质上是$MVP = Vector World^T$ View^T Projection^T，而由于列主是默认的，因此在GPU上看起来就像$MVP = V$ W V * P一样。本质上只是CPU端的转置结果。

这里Sophia Renderer采用第二种方式，即默认GPU端都为CPU端绑定结果的转置，因此选用左乘来得到正确结果。

Reference

1. Mathematics for 3D Game Programming and Computer Graphics, Third Edition, Section 5.4
2. Introduction to 3D GAME PROGRAMMING WITH DIRECTX® 11, Section 5.6

选择smallpt了作为Cuda Path Tracer初尝的借鉴，因此此次主要任务是对smallpt进行Cuda移植，并与好友shawnlu尝试性的做了部分GPU上的优化。代码已开源至smallptCuda

Cuda部分的入门教程较多，可以参考CUDA C/C++ Basics以及An Even Easier Introduction to CUDA

Benchmark

Cuda部分杂记

1. Cuda在Windows上会遇到Kernel执行时间过长而被结束进程的问题，可以参考Note中对核函数的监控项进行修改的操作。

2. 本例使用的helper_math.h可以在Custom Cuda Dir\CUDA Samples\v8.0\common\inc
   中找到，Cuda提供了基本的float3, int3之类的包装便于计算。

从OpenMp到Cuda

Cuda的部分难度主要是对于Grid, Block, Thread的理解上, 对于GPU与Cuda的抽象逻辑对应上可以参考Cuda的Threading: Block和Grid的设定与Warp。

总结一下，Warp是组成线程组的基本单位，一般为32，不足32的会以32个线程打包运行(有部分线程不工作，造成浪费)，一般而言BlockSize设定为256总体效果都还不错。SM会根据分配的Block消耗资源的多少来分配究竟有多少个Block在SM中。

具体的N卡核心数等属性信息，可自行获取cudaDeviceProp打印。具体属性值含义可参考cudaDeviceProp Struct Reference

和OpenMp这类CPU上的多核并行不同的是，在线程中并不确定执行顺序，因此需要知晓当前线程对应像素关系就需要threadIdx, blockIdx, blockDim, gridDim等变量来算出。这部分在CUDA C/C++ Basics有简介。

失败的优化

在参考Yining Karl Li的报告后，曾尝试转变原有的基于像素的并行转为基于光线的并行，核心思想就是通过预分配光线，将光线的深度iteration拆分为广度每循环一次加深一层并做stream compaction减少光线数量。

可查看dev分支的历史commit查看具体实现

这里遇到了两个问题

1. 未预估到光线的占用内存情况，按照下方的Ray布局一根光线将会占用60B, 取SPP为2048为例每个像素将预分配SPP根光线，需要$1024$7681024*60=45G的显存。

struct Ray
{
    float3 origin;
    float3 direction;

    int depth, pixelIndex;
    float3 throughput, L;
};

即便是最简形式的Ray，也仍然占用12B，上述分辨率下也需要占用9G显存，GTX750上的2G显存远远不够(好友的GTX1080ti 12G显存面对45G这样的压力也完全不够)。

struct Ray
{
    float3 origin, direction;
};

2.Cuda中Thrust的Stream Compaction本身并行效率很可观(优化原理可参考Yining Karl Li的报告)，但此法其实更适合于实时光线跟踪，对于目前的GPU纯计算而言，不仅仅增加了Device与Host之间的带宽开销，增加了多次Kernel启动消耗，更增加了线程需要从Global Memory多次读写数据的开销(且存在线程竞争情况)。甚至降低的光线数量带来的性能优化完全不足以弥补。

// cast all rays we need
initRays<<<A, B>>>();

// Russian Roulette would stop ray
while(1)
{
    rayStep<<<C, D>>>();

    // reduce the count of ray
    streamCompaction();
}

最后dev版本放弃了Stream Compaction，改用如下方式，但初始化分配光线仍然需要巨大资源消耗，且在ray结束迭代需要将结果存入放在Global Memory上的output缓冲区时，需要做原子操作以免出现竞争问题(进一步带来了消耗)。

// cast all rays we need
initRays<<<A, B>>>();

// Russian Roulette would stop ray
rayIterate<<<C, D>>>();

由于相比于基于像素并行带来的额外内存开销，整体性能倒退2x左右。原本只是希望展开GPU线程中忙忙的for(spp)繁重的循环已达到性能优化，但基于光线的并行的确更适合实时光线追踪而非纯GPU渲染。

内存上的优化

并行效率难以优化的前提下，内存优化是突破口。由于GPU的Cache过小，不会做类似CPU上的多级Cache块调入优化，Global Memory类似于CPU上的内存，Shared Memory便可充当Register或Cache的地位(Shared的速度最优情况下接近寄存器)，Global与Shared区别可参考Stackoverflow。

这里做的本质上就是手工模拟Cache与内存块交换思想。以如下输出结果至缓冲为例，

__shared__ float3 temp;
temp = // do some assignment;
// output on global memory
output[i] = temp;

先将结果存入shared上的temp，再转入global上的output，思想类似于多级cache(其余sheard部分优化类似)。还对基本的类型做了内存对齐。但由于光线跟踪带宽要求并不高，所以最后结果优化并不明显，不过仍然有1s左右的提升。