[ Bingo ]

网易游戏面经

为记录第一次在网易游戏电面PC客户端游戏研发职位的博客。

离线渲染部分

以下问题针对PBRT而言

1.BRDF的单位是什么?

开口跪

2.渲染方程中左边那一项 $Lo(p, \vec{wo})$ ，具体的含义是什么。是irradiance还是radiance，他们具体的单位又是什么？

概念回答的还算准确，但是他们具体的单位又说的有点模棱两可，后来发现其实也没有说错。

3.BRDF和pdf的关系是什么?

我回答的是 $E = \frac{1}{N} \sum\frac{f(p, \vec{w_i}, \vec{w_o})}{pdf()}$ 的解读，但具体有何联系说的有点模棱两可，理解深度也是不够。

4.蒙特卡洛方法是如何实现Ray Tracing的，或者说蒙特卡洛方法是怎样得到最终结果的?

回答的乱七八糟，语言逻辑组织的很有问题。对蒙特卡洛的理解深度还是不够。

5.Russian rulette的具体作用是何?

这里我提到是减小方差，但事实上作用不仅如此。是因为挑选出了重要的光路。

6.你的渲染器是如何实现高光项的?

这一提问没答好，事实上后来想了一下，可以回答Atoms折射模型里，用菲涅尔项算出反射概率用此概率计算反射项即可。

7.微表面模型的具体方程?

只是提了一句微表面，以后不能作大死。不记得具体公式，只回答出了一个大体的概念。

8.irradiance和radiance各是什么？

概念是回答八九不离十，但是区别和单位上又犹豫了一段时间。

光栅化部分

以下全篇基本上都是gg状态，很久不搞光栅化，连基本概念都搞不清了。

1.光栅化的含义?具体的过程是怎么样的?

说了一下就是把几何上的三角形转换成栅格化像素的过程,其他gg

2.你的软件光栅化，顶点在进行转换的时候，具体做了哪些事?

好几年没看了,只说出了把所有的模型对象全都转换到相机坐标下，问转换完之后做了什么就不记得了，gg

3.当时提了一个Phong模型，问我其他的模型的公式知道吗?

gg

4.齐次坐标如何表示点和矢量?为什么要这样表示?

只回答对了w项。具体为什么我说平移就用不了了，但是好像不是很对。gg

5.OpenGL和DirectX懂哪个?

GL不够深入,gg

C++部分

1.override和overload的差别?

一个是覆盖，一个是函数重载,可以见C++专题

2.override和哪个关键字是相对的?

final

3.为什么要写override关键字，会有什么好处或者不写有什么坏处？

只知道覆盖的作用，坏处gg

4.虚函数的实现机制?虚表里放了什么?有什么作用?

基类指针里存放了被覆盖的子类的虚函数指针

5.异常处理用过吗?智能指针用过吗，构造和赋值的时候具体都做了些什么事?

智能指针只知道引用计数，其他统统gg

具体问题

现有两个与坐标轴不平行的2D矩形，程序思想上如何实现矩形是否相交?

分离轴。

如何求点在直线上的投影点?

没想起来一个较好的，用了一个解析几何的办法。想了个点到直线距离，然后直角三角形的做法

有没有更好的办法，比如矢量的办法求?

没能现推出来一个好的。可见这个

总结

也是询问了一下面试官我自己未来应该如何学习，希望能够在pbrt上继续深入下去，pbrt很不错，他的同事也没有多少人看完了这本书。光栅化的不熟悉不行，要很熟悉光栅化那一套。

一句话就是，开口跪，全场懵逼，直接gg。

Unidirectional Path Tracing

Deprecated(2017.03.30)

本文讲述的是在实现Atoms渲染器基于物理部分遇到问题的PBRT笔记解读

Atmos最先尝试实现的，是最最简单的路径追踪思想，也就是递归。搭配蒙特卡洛方法来计算渲染方程的无穷积分，本质上的思想是非常浅显易懂的。但这里我遇到了一个问题。

$L_o(p, \vec{w_o}) = L_e(\vec{w_i}, p, {w_o}) + \int_{\Omega}{BSDF(\vec{w_i}, p, \vec{w_o})L_i(\vec{w_i}, p)cos\theta d\vec{\omega}}$

首先是将简单的递归改写成非递归的积分器Intergrator形式遇到了问题：单项路径追踪如何写成非递归样式？

其次是，为何Mitsuba与pbrt的Interator中Path Tracer实现中都有Direct illiumination过程，难道直接寻找光源进行求解计算不是Bias的？

尝试求解无果后，带着疑问又重新拾起当初一知半解看了大概的pbrt。

$P_{763}$ 中的路径追踪最经典算法

$\frac{1}{1-q_1}(P(\bar{p_1} + \frac{1}{1-q_2}(P(\bar{p_2})+\frac{1}{1-q_3}(P(\bar{p_3}+…,)))$

PBRT中多次强调，递归计算出来的单项路径追踪最大的问题在于他的n个光线相交点的最后那一个，一定得是在光源上。否则，整条路径在最初点上的光照贡献就是 $0$ 。

这个概念非常易懂，但也正是这个特性，导致最最浅显概念上的非递归版本的单向路径追踪务必要额外增加一个栈来存放所有BSDF信息，这无疑只是简单的将递归转换一种写法，本质上并没有思想上的转换。

而真正核心的一句话，出现在 $P_{767}$ 的伪代码中。

Possibly add emitted light at path vertex

明白直接光照计算方式的都知晓当前相交点使用Multiple importance sampling这一点，其最关键的就是主动向光源上计算贡献。

PBRT中分为两种采样方式，第一种适合光源较多的场景，是直接对场景中所有光源进行直接采样并累加最后求取期望，也就是 $E[f(x) + g(x)]$ ；蒙特卡洛表示这个求取方法在光源非常多的时候并不理想，这个期望也可以通过 $E[f(x)]+E[g(x)]$ 来完成，因此可以在场景中随机选取一个光源计算其贡献。

这里主动的求光源的光照贡献，其实和点光源/面积小的光源做法是一模一样的。

点光源 / 面积很小的光源会出现一个问题，就是单向路径追踪时，击中光源的概率实在太低了，在点光源上这个概率甚至是0！因此主动求取其光照贡献乘以所谓的权重依旧能保持无偏，但却解决了一个场景中只有点光源时无法照亮任何物体的问题。

$P_{764}$ : In a similar manner, small area light sources can also be source of variance if not sampled explicityly.

改进后的单向路径追踪的算法改写为

$\frac{L_e(p_i \to p_{i-1})f(p_i \to p_{i-1} \to p_{i-2}|cos\theta_{i-1}|)}{p_A(p_i)}(\prod^{i-2}_{j=1}\frac{f(p_{i+1} \to p_j \to p_{j-1})|cos\theta_j|)}{p_{\omega}(p_{j+1}-p_j)})$

括号的左项就是代表了随机采样的光源的贡献(BSDF在光源-当前点上的f，乘以光源向相交点的 $L_e cos\theta$ )，右方式子代表了BSDF采样的贡献累乘，由于每次循环所做的事情都一样。因此很自然的就可以写成非递归的形式。

可以看到这里直接寻找光源计算贡献的过程依然是Unbiased，只不过将最后击中光源的这一步操作分配到了路径的各个部分上而已。

假定最后一次光线在光源上相交点为 $p_i$ ，那么这一次的光源经常是会被忽略掉的。因为光源的贡献在上一个光路上已经计算过一次，也就是从表面 $A$ 上的 $p_{i-1}$ 的光源贡献是对整条路径而言的。

有两个例外，当光路从摄像机/Eye中发出直接击中光源时，此时光源的贡献是不被忽略的。还有一个就是PBRT中提到的Specular表面。因为在非指定光路的入射角度上，得到的BSDF采样结果都是0，只因在上一步的计算中，这一过程是被直接浪费掉的(光源贡献为0)。因此需要在找到新光路之前，补上这一部分的光照贡献(实现思路与点光源类似)。

最后上Path Tracing核心伪代码(来自PBRT)

Spectrum Li(param)

// Get information from first ray object intesection
<Declare common path integration variables>

    for(int bounces = 0;; ++bounces)
        // Direct illumination
        <Possibly add emitted light at path vertex>
        <Sample illumination from lights to find path contribution> 

        // BSDF Sampling
        <Sample BSDF to get new path direction> 

        // Russian rulette / Max depth
        <Possibly terminate the path>

        // Indirect illumination
        <Find next vertex of path>

return L

Möller-Trumbore algorithm

本文为学习Möller-Trumbore算法的笔记，这里不对前面重心坐标求交进行记录，较为简单可自行推导。

根据中心坐标系可以很轻松的得出

$P = (1 - u - v)A + uB + vC$

这里P为射线与三角形相交点。u, v为以三角形两边为坐标系轴的P的投影长度(也可以理解为是P与该边两点连线三角形的面积与整体之比)。

$P=A - uA - vA + uB + vC = A + u(B - A) + v(C - A)$

而 $P=O+tD$ ，因此代入可得

$\begin{array}{l}O+tD & = & A + u(B - A) + v(C - A)\\O-A & = & -tD+u(B-A)+v(C-A)\end{array}$

这里转换为线性方程组的形式

$\begin{bmatrix}-D & (B-A) & (C-A)\end{bmatrix}\begin{bmatrix}t\\u\\v\end{bmatrix}=O-A$

那么问题就转化为如何求解出这里的 $t$ $u$ $v$ 三个分量

运用克莱姆法则

令 $M$ = $\begin{bmatrix}-D & (B-A) & (C-A)\end{bmatrix}$ , 也就是将上式的 $O-A$ 作为替换项，依次替换 $M$ 中的 $-D$ ， $B-A$ , $C-A$ ，得到 $M_t, M_u, M_v$ 。那么最终 $t = \frac{M_t}{M}, u = \frac{M_u}{M}, v = \frac{M_v}{M}$ 。理所当然的可以写为下面这类形式

$\left[ \begin{array}{r} t \ u \ v\end{array}\right] = {1 \over \left[ \left| \begin{array}{r} -D & (B-A) & (C-A) \end{array}\right| \right]}\left[ \begin{array}{c}\left| \begin{array}{c} O-A & B-A & C-A\end{array}\right| \ \left| \begin{array}{c} -D & O-A & C-A\end{array}\right| \ \left| \begin{array}{c} -D & B-A & O-A\end{array}\right| \ \end{array}\right]$

原文在这里使用了变量替换，本质一致

Scalar triple product很好理解，本质上就是计算一个平行六面体的体积，无论是先进行何方向上的叉积点积，最终计算的都是平行六面体的体积。

纯量三重积最重要的一点就是 $A \ldotp (B \times C) = det \left[ \begin{array}{c}\begin{array}{c} a_1 & a_2 & a_3\end{array} \ \begin{array}{c} b_1 & b_2 & b_3\end{array} \ \begin{array}{c} c_1 & c_2 & c_3\end{array} \\\end{array}\right]$

$D = B \times C = \left[\begin{array}{c} b_yc_z-b_zc_y & b_zc_x-b_xc_z & b_xc_y-b_yc_x\end{array}\right]$

那么

$A \ldotp D = \left[ \begin{array}{c} a_x& a_y & a_z \end{array} \right] \ldotp D = a_xb_yc_z + a_yb_zc_x + a_zb_xc_y - a_zb_yc_x - a_yb_xc_z - a_xb_zc_y$

对比行列式结果与上式，发现一致。

根据纯量三重积的结论，可以推出

$\left[ \begin{array}{r} t \ u \ v\end{array}\right] ={1 \over {(D \times (C-A)) \cdot (B-A)}}\left[ \begin{array}{c}((O-A) \times (B-A)) \cdot (C-A) \\(D \times (C-A)) \cdot (O-A) \\((O-A) \times (B-A)) \cdot D\end{array}\right]$

注意这里已经通过交换叉积顺序抵消 $-D$ 前方的负号了

最终实现代码

bool rayTriangleIntersect( 
    const Vec3f &orig, const Vec3f &dir, 
    const Vec3f &v0, const Vec3f &v1, const Vec3f &v2, 
    float &t, float &u, float &v) 
{ 
    // ---1
    Vec3f v0v1 = v1 - v0; 
    Vec3f v0v2 = v2 - v0; 
    Vec3f pvec = dir.crossProduct(v0v2); 
    float det = v0v1.dotProduct(pvec); 

    // if the determinant is negative the triangle is backfacing
    // if the determinant is close to 0, the ray misses the triangle
    if (det < kEpsilon) return false; 
    float invDet = 1 / det; 

    // ---2
    Vec3f tvec = orig - v0; 
    u = tvec.dotProduct(pvec) * invDet; 
    if (u < 0 || u > 1) return false; 

    // ---3
    Vec3f qvec = tvec.crossProduct(v0v1); 
    v = dir.dotProduct(qvec) * invDet; 
    if (v < 0 || u + v > 1) return false; 

    // ---4
    t = v0v2.dotProduct(qvec) * invDet; 

    return true; 
#else 
    ... 
#endif 
}

这里第一步先行计算 ${1 \over {(D \times (C-A)) \cdot (B-A)}}$ 中的分母是否为0，来判断三角形平面与射线方向是否平行。从分母的几何意义上说，根据交换律本质上原式也等价于 $D \ldotp ((C-A)\times(B-A))$ ，而D的右项即为法线(具体看左右手系)

我这里选取右手系，因为计算得到的法线为反的，因此这里在判断 $det$ 的正负时要看具体左右手系。

得到了det之后就按照克莱姆法则依次计算出t, u, v即可。先行判断 $u, v$ 的取值范围就是用于判断相交点P是否在三角形内。

Depth of Field

以下理解均来自PBRT以及网络资源

首先，对普通的品红相机添加景深不是一件非常困难的事情，在这里不赘述景深的生成原理，直接步入实现部分。

正常的品红相机为小孔成像，因此没有景深的概念，而增加一凸透镜之后，那么在焦平面左右的对象成像为清晰的，其余部分根据距离焦平面距离模糊程度不同。

如图所示，

点 $p_1$ 与 $p_2$ 在成像平面上根据离焦平面位置的不同对应的成像点也略有不同。

若有成像平面上一点 $p$ , 其光路经过凸透镜任意位置，最终都将「收敛」/「汇集」的一平面上，这一平面就是焦平面，有 $\frac{1}{s} + \frac{1}{i} = \frac{1}{f}$ 的关系(透镜公式)。

那么在计算机中，虚拟成像平面与焦平面位于同一侧，此时可这样理解光路：

多术光从凸透镜任意位置发出，击中成像平面的某一特定位置 $p$ ，终将在焦平面(focal plane)上某一点 $p'$ 汇聚。如图所示。

计算机中相机模型生成景深原理就是上图。

PBRT中景深的实现

// 1.于透镜上采样
float lensU, lensV;
ConcentricSampleDisk(sample.lensU, sample.lensV, &lensU, &lensV);
lensU *= lensRadius;
lensV *= lensRadius;

// 2.计算当前采样点在焦平面上对应的收敛点
float ft = focalDistance / ray->d.z;
Point Pfocus = (*ray)(ft);

// 3.更新相机射出光线信息
ray->o = Point(lensU, lensV, 0.f);
ray->d = Normalize(Pfocus - ray->o);

步骤2 3难度不大，其原理就是相似三角形。因为凸透镜上任意光路都会在焦平面汇集，因此为了快速计算得到焦平面上的点，我们直接选取光路从film上点A经过凸透镜中心的方向来得到与焦平面的交点(凸透镜中心不会发生折射现象，也就无需使用Snell公式计算出射光线方向)

难点在于第一步ConcentricSampleDisk。要求是在圆形透镜上随机采样，而问题出在我们的采样点分布在方形区域内，目标区域为圆形，因此需要做一次映射。

原论文实现地址A Low Distortion Map Between Disk and Square。其作用就是在将笛卡尔坐标系下的随机点 $p\in[-1, 1]$ 转换为极坐标，确保正方形区域能够直接映射为极坐标。

传统方法映射笛卡尔坐标至极坐标，转换较为简单。但问题在于无法均匀分布采样点，中心点区域会发生过采样问题。如图

// Draw two uniform random numbers in the range [0,1)
R1 = RAND(0,1);
R2 = RAND(0,1);

// Map these values to polar space (phi,radius)
phi = R1 * 2PI;
radius = R2 * r;

// Map (phi,radius) in polar space to (x,y) in Cartesian space
x = cos(phi) * radius;
y = sin(phi) * radius;

图来自Concentric Disk Sampling

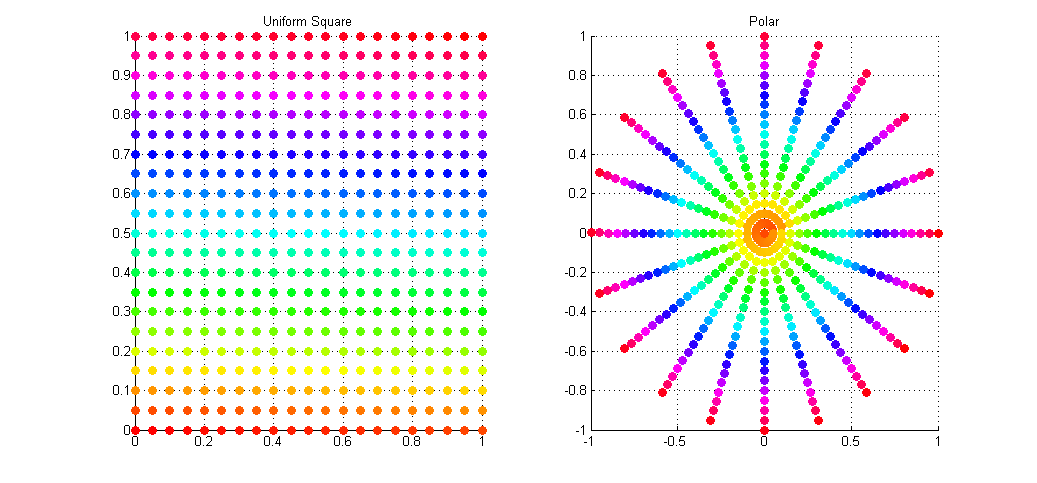
因此论文A Low Distortion Map Between Disk and Square的优势就在于可以将笛卡尔坐标系下均匀分布的随机点映射至极坐标系下且不会发生过采样问题。如图

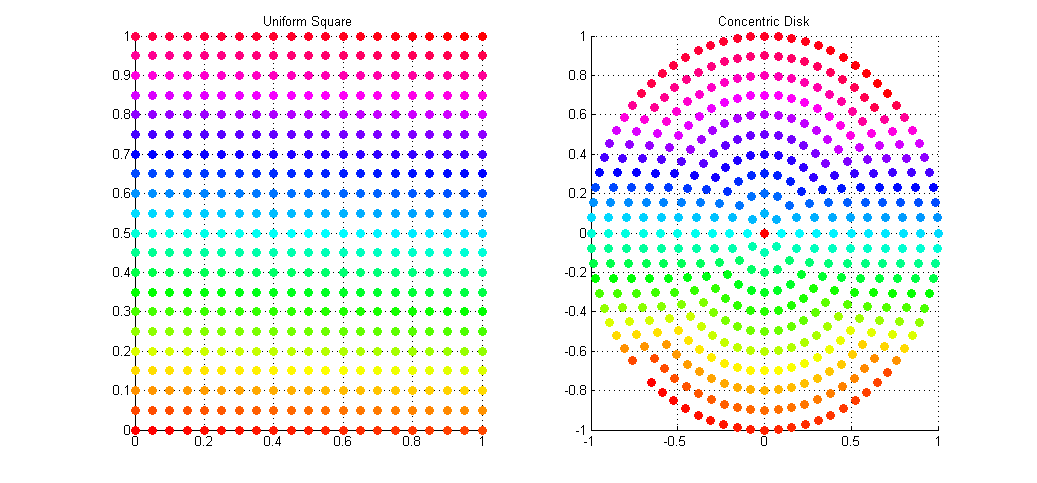
可以通过直接观察颜色点的对应位置做对比

算法分析如下

核心思想本质上就是将方形区域与圆形区域做区域划分

若给定两随机数 $a, b\in[0, 1]$ ，那么首先可以将其映射至 $[-1, 1]$ 范围内。可见上方左图显示。

Region 1

这块区域可由直线 $b = a(a>b)$ 与直线 $b = -a(a>-b)$ 确定，也就是代码中if-else环节所做的工作。

以下思想很关键，这里视a为极坐标半径，b为对应圆弧长度。那么可得 $r = a, \phi = \frac{\pi}{4} \ldotp \frac{b}{a}$

检验，当 $a = 0.4, b = 0.2$ 时，可得 $r = 0.4, \phi = \frac{\pi}{8}$ ；当 $a = 0.4, b = -0.2$ 时，可得 $r = 0.4, \phi = -\frac{\pi}{8}$ 与逻辑推导吻合。

同理，根据每个区域的 $a,b$ 绝对值关系，推出Region 2: $r = b, \phi = \frac{\pi}{4} \ldotp (2-\frac{b}{a})$ , Region 3: $r = -a, \phi = \frac{\pi}{4} \ldotp (4+\frac{b}{a})$ ，Region 4: $\frac{\pi}{4} \ldotp (6-\frac{b}{a})$ 。

可以自行确定 $\mid a\mid$ 与 $\mid b\mid$ 之间的关系

再加上最后一个圆心处, $r = 0, \phi = 0$ ，即可构成完成的笛卡尔坐标映射至极坐标的任务。

测试结果如下，左图为均匀分布随机采样点，右图为(使用OF 0.9.0做打点测试)，直观的看到非常吻合和算法本身实现效果。

最后上OF实现代码

ofVec2f squareToUniformDisk(const float sampleU, const float sampleV, int type)
{
    float phi, r, u, v;
    // (a,b) is now on [-1,1]ˆ2
    float a = 2 * sampleU - 1;
    float b = 2 * sampleV - 1;

    // region 1 or 2
    if(a > -b)
    {
        // region 1, also |a| > |b|
        if(a > b)
        {
            r = a;
            phi = (PI / 4) * (b / a);
        }
        // region 2, also |b| > |a|
        else
        {
            r = b;
            phi = (PI / 4) * (2 - (a / b));
        }
    }
    // region 3 or 4
    else
    {
        // region 3, also |a| >= |b|, a != 0
        if(a < b)
        {
            r = -a;
            phi = (PI / 4) * (4 + (b / a));
        }
        // region 4, |b| >= |a|, but a==0 and b==0 could occur.
        else
        {
            r = -b;
            if(b != 0)
                phi = (PI / 4) * (6 - (a / b));
            else
                phi = 0;
        }
    }

    u = r* cos(phi);
    v = r* sin(phi);
    return ofVec2f(u, v);
}