GGX Spherical Area Light
Introduction
离线渲染中,对于面积光的渲染也有较多研究,多为在面积光源形状上做采样,配合BRDF进行MIS,但这在实时渲染中要想收敛则采样数过多开销过大。
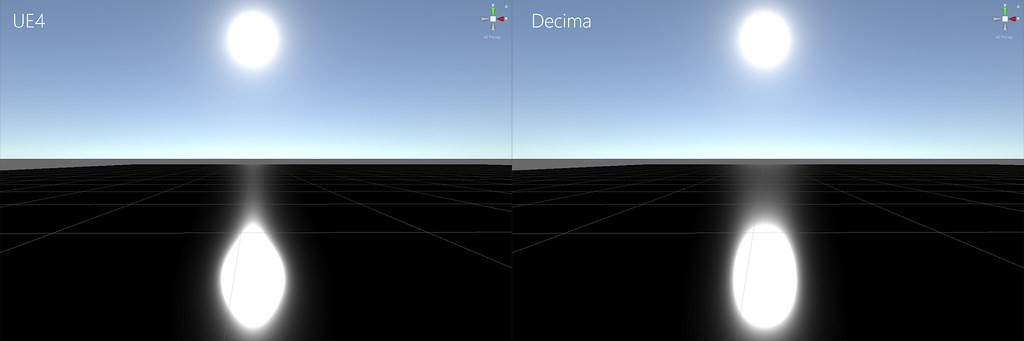
Eric Heitz曾对多边形的实时面积光渲染做出较好的模拟,对球面积光的近似多采用Karis在13年发布的Representative Point Method,其实现较为高效又兼容GGX微表面被广泛采纳。Decima在Siggraph 2017上又对其进行了改进,使其在边缘处拖尾更接近Reference(如图)。
但无论是UE4或是Decima都无法保证Physically Based,也就是不满足Energy Conservation,仅能实现较为近似的效果。因此这里不对Normalization Factor做过多记录。
Decima: We’re currently experimenting with alternative formulas for
normalization to better match our reference. This, however,is still in flux.
UnrealEngine: To derive an
approximate normalizationfor the
representative point operation we divide the new widened normalization factor by the original
Representative Point Method
Unreal Engine 4
Representative Point的核心思想就是使用一个点来模拟一个球面光的效果。在GGX BRDF计算中,光照方向不再固定,而是来自于球面,因此关键是如何确定光照方向。
// no more punctual light direction
float3 L = normalize(lightPoint - hitPoint);
// but get L from spherical area light
float3 L = getLightDirection(normalize(lightPoint - hitPoint), ...);
需要注意的是,此方法
对平行光同样有效(平行光本为点光无限远的近似),仅需将原始L改为平行光方向即可。
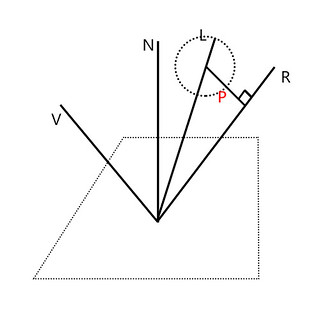
Karis提出的解决上述问题的核心思想是,当反射光向量R与球相交,则此时R就是光照方向向量。R处于球外时,若为离线渲染中,则此时应在球面上大量采样来求解对表面BRDF的贡献。由于为实时渲染,思路就是选取对表面光照贡献最大的点作为光照方向。此时选择球面上离反射向量R最近的点作为光照来源(如图)。
float3 getLightDirection(float3 L, float3 R, float radius)
{
float3 centerToRay = R * dot(L, R) - L;
// ray intersected / not intersected both combined(saturate)
float3 closestPoint = L + centerToRay * saturate(radius / length(centerToRay));
// the length of closestPoint could be used for normalization
return normalize(closestPoint);
}
上述UE4实现中,
已经包含了反射光与球相交/不想交的情况。因此仅需对GGX的光照来源进行改变即可快速模拟球面光。
UE4中的近似Normalization Factor选择如下,由于仅为近似解,因此PDF中也未包含详细推导
Decima
Decima的近似实现也沿用了UE4的方法,变化的是选取光照来源位置不再是反射光线最近的点,而是能使得最大的点(GGX高光分布中N与H越接近,或者说R与L越接近则起光照在BRDF上的贡献最大,可自行查看Disney BRDF Explorer中GGX的分布)。
Decima采取如下方式选取光照方向
这里有一处微调,不再是向R投影,而是投影至Lc(如图)
取为一坐标系,在此圆盘上找到一个,使得达到最大的点。
由于可以万能表示, ,且在区间内单调递增,因此将求取转为求。且令(选此因为分式上含根号,且可直接将用于GGX的NDF计算上)
此处推导过于繁琐,因此未给出具体展开式
取
由于牛顿迭代可求函数根,对做多次迭代则可收敛至根值。此时要求最大值,因此对进行牛顿迭代,则根值处为求得最大值。取为最终结果。
float GetNoHSquared(float radiusTan, float NdotL, float NdotV, float VdotL)
{
// See presentation for more deatil
}
void EvaluateNdotH(float radius, float roughness, float lightCenterDistance, float NdotL,float NdotV, float LdotV, inout float NdotH)
{
float radiusTan = max(0.001, radius / lightCenterDistance - roughness * 0.25);
NdotH = sqrt(GetNoHSquared(radiusTan, NdotL, NdotV, LdotV));
}
void EvaluateNormalizationFactor(float roughness, float LdotH, float radius)
{
// Decima: Still in flux
float roughnessSquaredLdotH = roughness * roughness * (LdotH + 0.001);
normalization = roughnessSquaredLdotH / (roughnessSquaredLdotH + 0.25 * radius * (2.0 * roughness + radius));
}
这里使用时,需格外注意提供给GGX计算的,除更改后的NdotH外,NdotL, NdotV, VdotL, LdotH中的L与H皆为初始方向,尽管这样会在Point垂直于Normal时失效,但仍然能取得较好的效果
ScreenShots
下图为Unity 2018中实现对比结果,可明显看见接近边缘处的拖尾更接近Reference,也就可以实现地平线中夕阳的拖尾效果。