Bingo, Computer Graphics & Game Developer

Atmosperical simulation

Introduction

本文基本理论及其实现参考GPU Gems 2[1]^{[1]}和Scratchapixel[2]^{[2]}

大气的效果主要是由大小的粒子经过大量散射后带来的结果。 其中光被分子大小的粒子散射称之为Rayleigh scattering，而更大一些的沙尘散射被称之为Mie scattering。 大气散射的结果主要是由这两部分组成。 本文未实现多重散射，以及点光源等更通用的方法，而是使用单级散射配合上平行光的结果。

Out-Scattering And In-Scattering

Out-Scattering

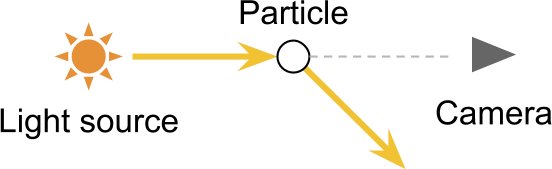
In-Scattering

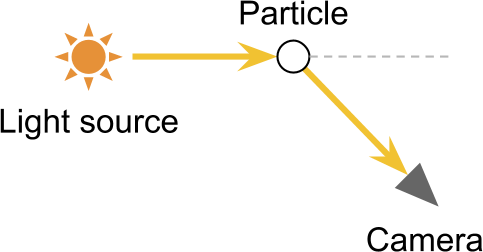
如若有一平行光(这里假定太阳无限远，则光源近似于平行光)入射大气相交C点，则由于Out-Scattering的影响光照强度将会有一定衰减，其中T为衰减系数。

IP=IC⋅T(CP→)I_P = I_C \cdot T(\overrightarrow{CP})

从P点的光照抵达A点时，会发生由P点的大气粒子经过散射造成的In-Scattering，从CP→\overrightarrow{CP}方向变为PA→\overrightarrow{PA}方向，散射系数定义为S，λ\lambda为光的波长，θ\theta为散射角度，hh为相对海拔高度。 同样也会由于在路径PA→\overrightarrow{PA}上造成衰减。

IA=IP⋅S(λ,θ,h)⋅T(PA→)I_A=I_P \cdot S(\lambda, \theta, h) \cdot T(\overrightarrow{PA})

S表示的是在某一方向上的散射系数，以Rayleigh scattering为例

S(λ,θ,h)=π2(n2−1)22ρ(h)N1λ4(1+cos2θ)S(\lambda, \theta, h)=\frac{\pi^2(n^2-1)^2}{2} \frac{\rho(h)}{N} \frac{1}{\lambda^4}(1+cos^2\theta)

Parameter Meaning
λ\lambda 入射光波长
θ\theta 散射角度
h 当前点的海拔
N 分子数量密度
ρ(h)\rho(h) 关于海拔1位置的相对密度

其中S(λ,θ,h)S(\lambda, \theta, h)可以拆分为三项，P(θ)P(\theta)就是体渲染中常见的Phase Function

S(λ,θ,h)=β(λ,h)P(θ)=β(λ)ρ(h)P(θ)S(\lambda, \theta, h)=\beta(\lambda,h)P(\theta)=\beta(\lambda)\rho(h)P(\theta)

无论是Mie还是Rayleigh其大气密度都随着海拔接近于指数下降

ρ(h)=e−hH\rho(h)=e^{-\frac{h}{H}}

Rayleigh Scattering And Mie Scattering

这里β(λ,h)\beta(\lambda,h)可以通过对S(λ,θ,h)S(\lambda, \theta, h)在整个球面上进行积分，以算出在总方向上的散射系数。 其中可以预计算完β=(33.1e−6,13.5e−6,5.8e−6)m−1\beta=(33.1e^{-6}, 13.5e^{-6}, 5.8e^{-6})m^{-1}

β(λ,h)Rayleigh=∫02π∫0πS(λ,θ,h)sinθdθdϕ=π2(n2−1)22ρ(h)N1λ4∫02π∫0π(1+cos2θ)sinθdθdϕ=8π3(n2−1)22ρ(h)N1λ4\begin{array}{l} \beta(\lambda, h)_{Rayleigh} &=& \int^{2\pi}_{0}\int^{\pi}_{0}S(\lambda, \theta, h)sin\theta d\theta d\phi\\[2ex] &=& \frac{\pi^2(n^2-1)^2}{2} \frac{\rho(h)}{N} \frac{1}{\lambda^4} \int^{2\pi}_{0}\int^{\pi}_{0}(1+cos^2\theta)sin\theta d\theta d\phi\\[2ex] &=& \frac{8\pi^3(n^2-1)^2}{2} \frac{\rho(h)}{N} \frac{1}{\lambda^4} \end{array}

大气中的吸收系数可以忽略不计，因此散射系数基本由Phase Function决定。 其对应的Phase Fucntion为

P(h)=S(λ,θ,h)β(λ)=316π(1+cos2θ)\begin{array}{l} P(h) & = & \frac{S(\lambda, \theta, h)}{\beta(\lambda)} \\[2ex] & = & \frac{3}{16\pi} (1+cos^2\theta) \end{array}

Mie Scattering不像Rayleigh那样，其大小变化也接近于从海拔1位置处指数下降，这里取β(λ,0)=210e−5m−1\beta(\lambda, 0)=210e^{-5}m^{-1}，g=0.76g = 0.76

β(λ,h)Mie=β(λ,0)⋅e−hHM\beta(\lambda, h)_{Mie}=\beta(\lambda, 0) \cdot e^{-\frac{h}{H_M}}

P(h)=38π(1−g2)(1+cos2θ)(2+g2)(1+g2−2gcos2θ)32,g∈(−1,1)P(h) = \frac{3}{8\pi} \frac{(1-g^2)(1+cos^2\theta)}{(2+g^2)(1+g^2-2gcos^2\theta)^{\frac{3}{2}}}, g \in (-1, 1)

Optical Depth

衰减指数T与海拔高度有关，非定值，因此需要在海拔上做积分

T(PA→)=e−∫PAβ(λ,h)ds=e−β(λ)∫PAρ(h)dsT(\overrightarrow{PA})=e^{-\int^A_P \beta(\lambda, h)ds}=e^{-\beta(\lambda)\int^A_P \rho(h)ds}

此处令光学深度D为

D(PA→)=∫PAρ(h)dsD(\overrightarrow{PA})=\int^A_P \rho(h)ds

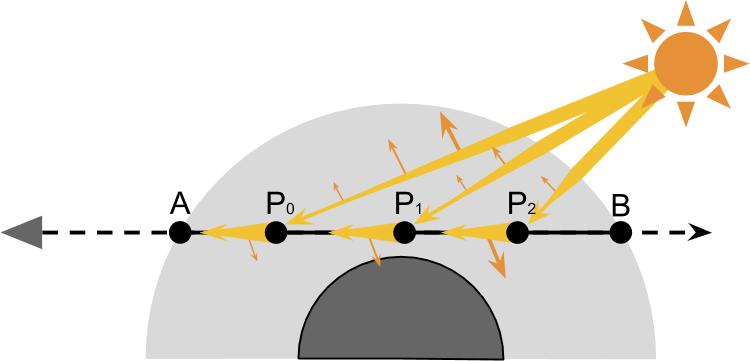
则最终进入到A处的光照为

IA=∫ABIP⋅S(λ,θ,h)⋅T(PA→)d=∫ABIC⋅T(CP→)⋅S(λ,θ,h)⋅T(PA→)ds=IC⋅β(λ)⋅ρ(h)∫ABe−β(λ)(D(CP→)+D(PA→))⋅ρ(h)ds\begin{array}{l} I_A &=& \int^B_A I_{P} \cdot S(\lambda, \theta, h) \cdot T(\overrightarrow{PA}) d\\[2ex] &=& \int^B_A I_{C} \cdot T(\overrightarrow{CP}) \cdot S(\lambda, \theta, h) \cdot T(\overrightarrow{PA}) ds\\[2ex] &=& I_{C} \cdot \beta(\lambda) \cdot \rho(h)\int^B_A e^{-\beta(\lambda)(D(\overrightarrow{CP}) + D(\overrightarrow{PA}))} \cdot \rho(h) ds \end{array}

Implementation

RayMarching

这里借鉴英伟达Demo，利用vs来生成一个全屏的三角形[10]^{[10]}，以方便在PS中RayMarching(因为在VS中无需任何输入)。 此处由于使用了真实的物理数值，因此在Shader实现中需要注意float会溢出的问题，可以通过暂存为double或做单位转换来解决

具体实现可参考Sophia渲染器中shader/skyRayCasting/部分

// vs 
struct output{ // something 
};

output main(uint id : SV_VertexID)
{
    output o;

    o.texCoord = float2((id << 1) & 2, id & 2);
    o.position = float4(o.texCoord * float2(2, -2) + float2(-1, 1), 0, 1);

    return o;
}

// ps
// do some ray march stuff

Mesh Based

这一部分其基本原理与上述是一致的，主要参考于GPU Gems 2[1]^{[1]}。 不同之处在于，Sean O’Neil提出了一个将大气预计算到LUT的方式，具体实现可以参考Sophia渲染器中shader/sky/部分

共计四张纹理，其中光学深度为HDR(部分会超过1)。 密度LUT中x表示海拔(映射为(0, 1))高度，y表示垂直角度(0时笔直朝上，1垂直向下)。 RGBA中Rayleigh与Mie各占一半，Rayleigh部分的密度以及Depth如下图

rayleigh lut

实现可以参考test中的earth的MakeOpticalDepthBuffer函数

Result

RayMarching结果较好，无论是在太空中或者是球内都有较为不错的结果

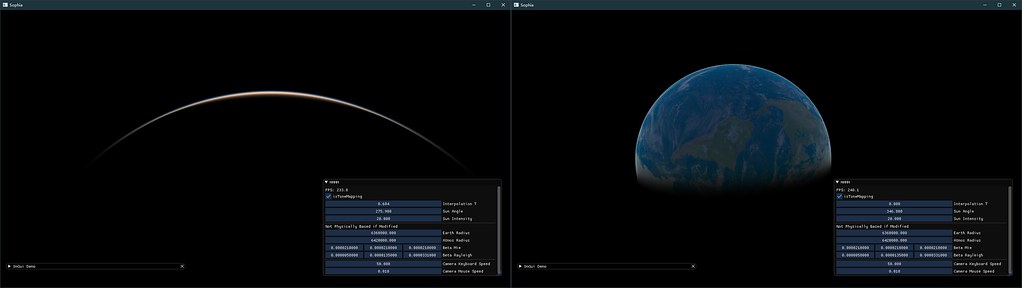
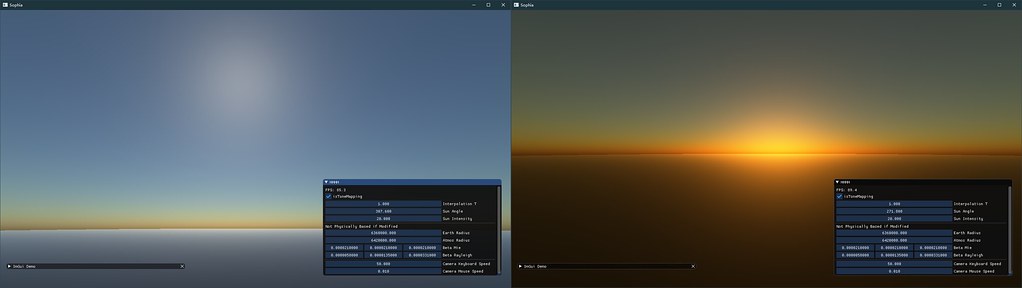
outside1 inside

Mesh Based远观效果是可以的，这里的球生成的时候只有64*64的细分程度，再配合上LUT，帧率能跑到1000+fps。 但其缺点是不可近看，在低面数下插值涂抹感比较严重，除非将球的面数成倍的增加，这样就带来了带宽和计算压力显得不是很必要(这里借鉴GPU Gems没有使用地球大小的参数，因此样式略微不同)

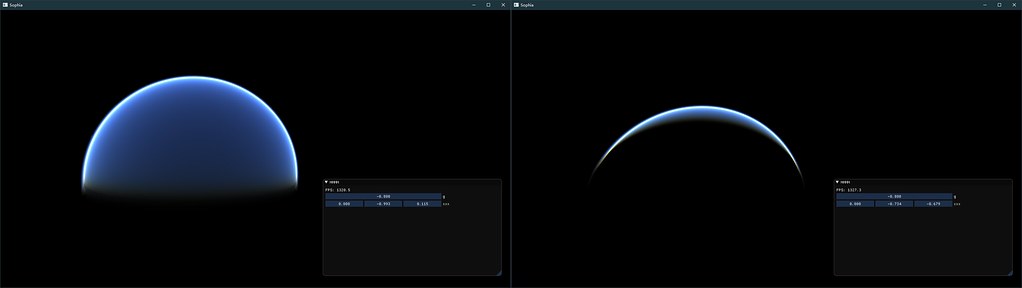
earth from space

因此最佳的方式应该是，RayMarching+LUT的实现方式(将在未来更新)。 原本做Mesh Based是希望能够将地面一次性也做displacement，不过由于效果一般，因此也没有做球内视角。

Reference

  1. GPU Gems 2: Accurate Atmospheric Scattering：基于Mesh的大气渲染模拟实现参考
  2. Simulating the Colors of the Sky：基本大气渲染理论推导参考
  3. Natural Earth III：地球纹理
  4. Practical Implementation of Light Scattering Effects Using Epipolar Sampling and 1D Min/Max Binary Trees
  5. Volumetric Atmospheric Scattering：大气理论推导及Shader实现参考
  6. Flexible Physical Accurate Atmosphere Scattering：预计算LUT对照参考
  7. 基于物理的大气渲染
  8. Display of the Earth Taking into Account Atmospheric Scattering
  9. Rendering Parametrizable Planetary Atmospheres with Multiple Scattering in Real-Time：93年 Nishita关于大气渲染的推导
  10. Vertex Shader Tricks：VS生成全屏Quad做单像素PS的解释